Animation of Partial Pressure of Gases

Introduction

This animation shows the evolution from atomic collisions of the partial pressure results associated with the perfect gas law. Importantly it also shows how to extend the usual three dimensional result to two and one dimension.

Standard Perfect Gas Laws

The total pressure due to a mixture of gases in a container is given by:

$P V = N k T$ (1)

where P is the pressure (N m^-2), V is the volume (m³) N is the total number of atoms in the volume, k is Boltzmann's constant, and T is the absolute temperature in degrees Kelvin. The partial pressure law is entirely similar to equation except that it expresses the pressure due to each atomic type, m, in the container.

$P_{m} V = N_{m} k T$ (2)

where P_m is the pressure due to the mth atomic type and N_m is the total number of atoms of the mth type in the container. In equations 1 and 2 it is assumed that atom-atom collisions have caused the temperatures (average energies) of all the atoms to become equal. In this animation, we will start with either all the atoms of a given type with either random or equal energies. The energy distributions of the atoms will, after a time, become the normal Boltzmann exponential where the exponential coefficient is the average energy.

Van der Waals recognized that in denser gases the total volume of the N atoms could become a substantial fraction of the total volume of the container and this fraction could modify equation 1 causing the pressure to have a more complicated dependence on N, atomic radius and volume. The modification is especially important when the gas density approaches that for a phase transition to a liquid. For the animation presented here we will assume that the gas is rarified enough that the modifications presented in the above link are not needed.

The perfect gas law presented in equation 1 is derived in the Appendix A for 3, 2, and 1 dimensional gases.

For completeness, since the perfect gas laws depend on energy equi-partition, Appendix B discusses how the energy distribution is computed from hard sphere collision kinetics and Appendix C discusses the hard sphere collision kinetics themselves.

Figures

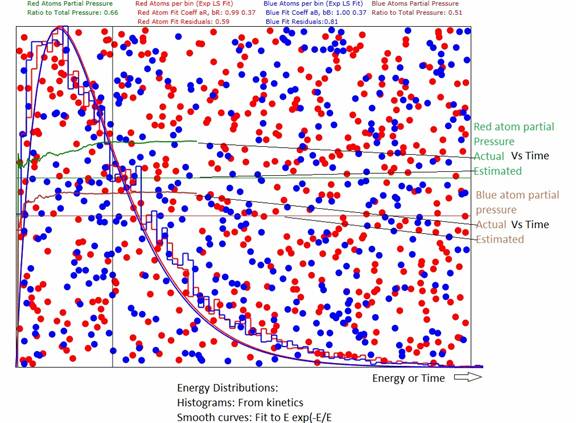
Figure 1: Showing results for 3D gas with 500 red atoms and 400 blue atoms. The estimated pressures are from and Appendix A. The actual pressures Vs time are computed from the momentum transferred to the walls of the container. The other curves are the energy distributions. The difference between estimated and actual is due to the rather small number of atoms in the samples.

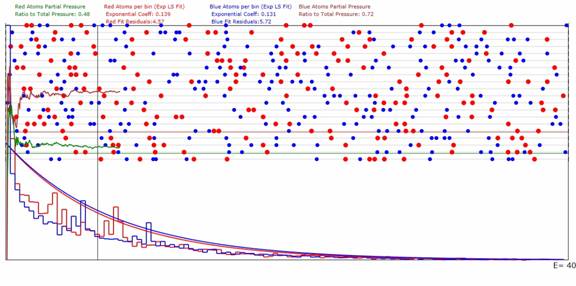
Figure 2: Same as Figure 1 except for being a 1D gas with 200 red atoms and 250 blue atoms. The results are for 20 Sub-Domains.

Computing the Pressure from the Motion of the Atoms

Three Dimensions

The pressure may be gauged by the force that the walls of the container has to apply in order to keep atoms that hit the wall inside the container. For this animation it will be assumed that the wall receives no energy from the atoms that collide with it. To keep it simple, we will consider the container to be a box of width X, height Y and depth Z. The amount of momentum change, dp, needed to reverse the motion of an atom colliding with the wall at x=X is

$d p = 2 m v_{x}$

where m is the mass of the atom and v_x is the x component of its velocity. If δn atoms hit an area δA of the X wall in time δt then the force per unit area (pressure) needed to reverse the x component of the momenta of all of them is:

$P = 2 \frac{δ n}{δ t δ A} m < v_{x} >$ (3)

where <v_x> is the average x component of the velocity for the n particles. Equation 3 has units of force per unit area and is the equation used by the animation program to compute the pressure when considering a 3 dimensional gas. The total area of our container is just

$A = 2 (X Y + X Z + Y Z)$

The program sums up all the collision momentum changes for all 6 walls during a single time interval and computes equation 3.

$P = \frac{2 m}{δ t} \frac{(\sum_{i} v_{x i} + \sum_{j} v_{y j} + \sum_{k} v_{z k})}{2 (X Y + X Z + Y Z)}$ (4)

Two Dimensions

For a two dimensional gas the depth can be considered to have gone toward infinity so that the areas of the Z walls are negligible compared to the X and Y walls. Then equation 4 becomes:

$P_{2 D} = \frac{2 m}{δ t Z} \frac{(\sum_{i} v_{x i} + \sum_{j} v_{y j} + \sum_{k} v_{z k})}{2 (X + Y)} \approx \frac{2 m}{δ t Z} \frac{(\sum_{i} v_{x i} + \sum_{j} v_{y j})}{p e r i m e t e r}$ (5)

where the definition of the perimeter, 2(X+Y), has been used and it should be remembered that the sum over v_z will be much smaller than the sums over v_x and v_y.

Also, for a 2 dimensional gas we need to determine the analog of the volume that was used in equation. Obviously, letting Z>> X,Y makes no difference in the volume:

$V_{2 D} = Z X Y$ .

However, to show that the results in 2D are consistent with equation 1, we should look at the ratio of P_2Dto P from equation 1. When this ratio is taken it cancels the Z dependence:

$\frac{P_{2 D C o m p u t e d}}{P_{T}} \approx \frac{\frac{2 m}{δ t Z} \frac{(\sum_{i} v_{x i} + \sum_{j} v_{y j})}{p e r i m e t e r}}{\frac{N k T}{X Y Z}} = \frac{2 m}{δ t} \frac{\frac{(\sum_{i} v_{x i} + \sum_{j} v_{y j})}{p e r i m e t e r}}{\frac{N k T}{X Y}}$ (6)

and therefore the new wall area for the 2D case becomes the perimeter, 2(X+Y), and the new volume in equation 1 becomes the area, XY. The units for 2 dimensional pressure are therefore force per unit length.

One Dimension

We will assume that the motion is in the x direction and, similar to the 2D case, let Y and Z be very large compared to X so that the areas XZ and XY are much smaller than YZ. Then the equations for the 2D case can be converted to following form:

$P_{1 D} \approx \frac{2 m}{2 δ t Z Y} (\sum_{i} v_{x i})$ (7)

The ratio of P_1Dto the P in equation 1 becomes:

$\frac{P_{1 D c o m p u t e d}}{P_{T}} \approx \frac{\frac{2 m}{2 δ t Z Y} (\sum_{i} v_{x i})}{\frac{N k T}{X Y Z}} = \frac{\frac{2 m}{2 δ t} (\sum_{i} v_{x i})}{\frac{N k T}{X}}$ (8)

so that the new effective volume for equation 1 becomes X and the new effective area becomes unity. The units for 1 dimensional pressure are therefore simply force.

But the force exerted by a particular atomic type on the end of the one dimensional domain depends on which type of atom happens to be closest to the particular end. So, in order to reduce statistical fluctuations of the partial pressures, we must separate the domain into a number M_s of equal sub-domains and compute the force at the ends of each. Since the average number of atoms in each sub-domain is reduced by the factor 1/M_s and the length of each sub-domain is also reduced by the factor 1/M_s, this division doesn't affect P_T in equation 1. However, the total forces on all the ends that result from equation 7 must be reduced by the factor 1/M_s since there are M_s more ends being impacted. Then equation 8 becomes:

$\frac{P_{1 D c o m p u t e d}}{P_{T}} \approx \frac{\frac{2 m}{2 δ t} (\sum_{i} v_{x i})}{M_{s} \frac{N k T}{X}}$ (7a)

Appendix A: Derivation of Equation 1

We want to be able to compare the numerically computed kinetic pressure results in the preceding section with the expected results from an analog of equation 1 which uses the average translational kinetic energy of the particles in place of a factor of kT, the thermal energy. For that reason, here I derive the analogs of equation 1 in 3, 2, and 1 dimension.

a. Three Dimensions

The time that elapses between a single atom's collisions on a single x=0 or x=X wall is

$δ t = \frac{2 X}{v_{x}}$

The momentum imparted by a single collision of an atom with the x=X wall is

$< δ p_{x} > = 2 m < v_{x} >$

and therefore the force due to a single atom imparted to the wall is

$F_{x} = \frac{< δ p_{x} >}{δ t} = \frac{m < v_{x}^{2} >}{X}$

However, since the energy is divided into 3 equal orthogonal (x,y,z) components we can now derive equation 1. The total average energy of the atom is

$E = \frac{m}{2} (< v_{x}^{2} > + < v_{y}^{2} > + < v_{z}^{2} >) = \frac{3}{2} m < v_{x}^{2} >$

so that F_x becomes:

$F_{x} = \frac{< δ p_{x} >}{δ t} = \frac{2 E}{3 X}$

and then the pressure on the x=X wall becomes

$P_{X} = N \frac{F_{x}}{A_{X}} = \frac{2 N E}{3 X Y Z} = \frac{2 N E}{3 V}$

Boltzmann's law states that each degree of freedom (e.g. E_x) carries kT/2 thermal energy.

$\begin{array}{l} \frac{k T}{2} = \frac{1}{2} m < v_{x}^{2} > = E_{x} \\ i . e . \\ E = \frac{3}{2} k T \end{array}$

so that finally we can write P_X in terms of the temperature and volume:

$P_{X} = \frac{N k T}{V}$

b. Two Dimensions

In the 2D case, the main change from the 3D case is that now the energy of a single atom is:

$E = \frac{m}{2} (< v_{x}^{2} > + < v_{y}^{2} >) = \frac{2}{2} m < v_{x}^{2} >$

However, since there are only 2 degrees of freedom we have that:

$E = k T$

and therefore the computed pressure is still the same:

$P_{X} = \frac{N k T}{X Y} = \frac{N k T}{A}$

where A is the area of the 2D domain and becomes the effective volume.

c. One Dimension

For the 1D case, there is a big difference because the only atoms that have access to the ends of the 1D domain are the 2 that are closest to the ends. Since the average spacing of atoms is X/N, the single end collision time for one of these atoms is therefore reduced to

$δ t = \frac{2 X}{N v_{x}}$

The force that a single atom exerts on its adjacent wall is

$F_{x} = \frac{2 m v_{x}}{δ t} = \frac{2 N m v_{x}^{2}}{2 X}$

For one dimension, the pressure is equal to the force and kT=1/2(m<v_x²>

$P_{x} = \frac{2 N m v_{x}^{2}}{2 X} = \frac{2 N k T}{X}$

which is really the same as equation 1 except for the factor 2 and the fact that now the effective volume is X.

Appendix B: Energy Distribution N(E)

The program uses the results for velocity changes that are given in the next section to compute the kinetic energies of all of the atoms at each time increment. These energies are used to compute a bin number, b

$b = \frac{E}{E_{\max}} n_{b i n s}$

where E_max is several times larger than the average energy of all the atoms and n_bins is the number of energy bins that we use.

When an atom has bin number b, an integer array component, iE_b, is incremented by an the integer 1. After all of the atoms have been polled, iE contains the distribution of number of atoms Vs atom energy, N(E). But, since we use 80 bins and we are limited to only about 1200 atoms, that would result, if N(E) is constant, in an average bin population of 15. The variance of 15 is about 4 and this would result in very erratic N(E). What we really want to know is the relative average occupancy of the energy bins. To obtain the final relative occupancy of the bins, it is acceptable to keep incrementing iE_b after each time interval. If we do this for a very large number of time increments, the initial transient changes of N(E) will be "averaged out". It is equivalent to taking many "snapshots" of the atomic energy distribution and averaging the results for each bin. Then what is plotted as a histogram is

$i E_{b} = \frac{1}{T} \sum_{t = 1}^{T} i E_{b, t}$

where t is the snapshot number and T is much greater than one.

The animation makes separate histograms for red and blue atoms. In addition, a least squares fit of an exponential function (the Boltzmann distribution) to the data in the histogram is made. The relative occupancy number (RON) equation is:

$N_{a} (E) = N_{0} \exp (- \frac{E}{< E >})$

where <E> is the average energy of the entire atom ensemble just as expected for a Boltzmann distribution. The animation shows beyond doubt that the RON equation has the same form and constants for red and blue atoms regardless of their masses, numbers and initial energies.

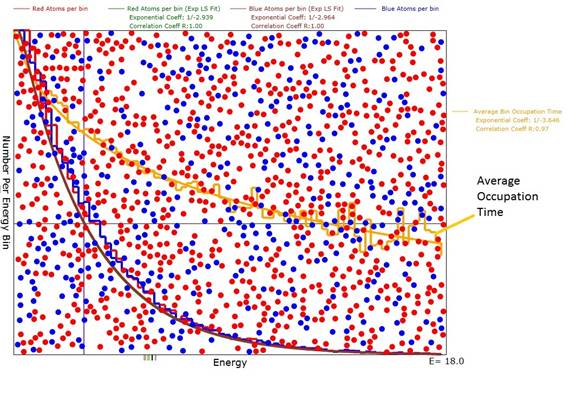
Figure 1: Diagram of the animation after evolution was reasonably complete with an average energy <E>=3.0. Note that the green and purple exponential plots are a good fit to the red and blue atom numbers per bin histogram with correlation coefficients of 1.0. Also note that the exponential coefficients were very close to -1/3.0 as expected for a Boltzmann distribution.

Appendix C: Mathematics of Hard Sphere Scattering

Atom-Atom Collisions of Different Mass and Velocity

Here we will consider spherical atoms which have the different masses, m₁ and m₂, and diameters, D₁ and D₂. The centers of the spheres will be labeled (x₁,y₁,z₁) and (x₂,y₂,z₂). Upon collision, the momentum transferred between the spheres will always be along the unit vector between their centers:

$u = \frac{[(x_{1} - x_{2}) \hat{x} + (y_{1} - y_{2}) \hat{y} + (z_{1} - z_{2}) \hat{z}]}{r_{12}}$ (2)

where

$r_{12} = \sqrt{{(x_{1} - x_{2})}^{2} + {(y_{1} - y_{2})}^{2} + {(z_{1} - z_{2})}^{2}}$

is the distance between centers. Since the animation is illustrated in only 2 dimensions, the collision analysis will assume a containing box that is large in the x and y dimensions but very thin in the z dimension. The following vector mathematics is correct for either 2 or three dimensions.

The expression for the final momenta in terms of the initial momenta is:

$m_{1} v_{1}^{'} + m_{2} v_{2}^{'} = m_{1} v_{1}^{} + m_{2} v_{2}^{}$ (3)

where the apostrophe on the left side of the equations indicates the final velocities. We know that the energies are conserved so

$\frac{m_{1} v_{1}^{' 2} + m_{2} v_{2}^{' 2}}{2} = \frac{m_{1} v_{1}^{2} + m_{1} v_{2}^{2}}{2}$ (4)

The directions of the change in momenta are along the vector of centers, u, and the values of the changes of momenta must be equal and opposite.

$m_{1} Δ v_{1} \equiv M δ v u = - m_{2} Δ v_{2}$ (5)

where M has units of mass and is still to be determined. Using equation 5 in equation 3:

$\begin{array}{l} m_{1} v_{1}^{'} = m_{1} v_{1}^{} + M δ v u \\ m_{2} v_{2}^{'} = m_{2} v_{2}^{} - M δ v u \end{array}$ (6)

Now we can use equation 6 in equation 4 to solve for the value of Mδv.

$\frac{(m_{1} v_{1}^{} + M δ v u) • (m_{1} v_{1}^{} + M δ v u)}{2 m_{1}} + \frac{(m_{2} v_{2}^{} - M δ v u) • (m_{2} v_{2}^{} - M δ v u)}{2 m_{2}} = \frac{m_{1} v_{1}^{2} + m_{2} v_{2}^{2}}{2}$ (7)

where the large dot stands for the dot product and equation 7 simplifies to:

$\begin{array}{l} \frac{(2 m_{1} M δ v u • v_{1}^{} + M^{2} δ v^{2})}{2 m_{1}} + \frac{(- 2 m_{2} M δ v u • v_{2}^{} + M^{2} δ v^{2})}{2 m_{2}} = 0 \\ M^{2} δ v^{2} (\frac{1}{m_{1}} + \frac{1}{m_{2}}) + 2 δ v M (u • v_{1}^{} - u • v_{2}^{}) = 0 \\ M δ v = \frac{2 m_{1} m_{2} u • (v_{2}^{} - v_{1}^{})}{m_{1} + m_{2}} \end{array}$ (8)

We can now make the identification:

$M = \frac{2 m_{1} m_{2}}{m_{1} + m_{2}}$ (9)

where M is known as the "reduced mass".

Equations 6 and 8 are a complete solution for the final momenta. The final velocities are computed by dividing both sides of equations 6 by their respective masses:

$\begin{array}{l} v_{1}^{'} = v_{1}^{} + \frac{2 m_{2}}{m_{1} + m_{2}} u • (v_{2}^{} - v_{1}^{}) u \\ v_{2}^{'} = v_{2}^{} - \frac{2 m_{1}}{m_{1} + m_{2}} u • (v_{2}^{} - v_{1}^{}) u \end{array}$ (10)

Suppose m₂>m₁. Then we see that the magnitude of the speed added to molecule 1 will be larger than the magnitude of the speed removed from molecule 2. We can easily see from equation 7, even though the averages of the dot products are zero, that, on average, the collision results in an increased kinetic energy for atom 1 and a decreased kinetic energy for molecule 2 because of the mass term in the denominators.

Summary of Results for Average Energies After Collision

After a collision with initial energies E₁₀ and E₂₀ we obtain the following results:

$\begin{array}{l} E_{1} = E_{10} + M δ v u • v_{1}^{} + \frac{{(M δ v)}^{2}}{2 m_{1}} = E_{10} + M [u • (v_{2}^{} - v_{1}^{})] (u • v_{1}^{}) + \frac{M^{2}}{2 m_{1}} [^{u • (v_{2}^{} - v_{1}^{})] 2} \\ E_{2} = E_{20} - M δ v u • v_{2}^{} + \frac{{(M δ v)}^{2}}{2 m_{2}} = E_{20} - M [u • (v_{2}^{} - v_{1}^{})] (u • v_{2}^{}) + \frac{M^{2}}{2 m_{2}} [^{u • (v_{2}^{} - v_{1}^{})] 2} \end{array}$ (11)

When the above result is averaged over all angles between u and v_i that actually lead to a collision i.e. u.(v₂-v₁)<0 we obtain:

$< E_{1} > = E_{10} - \frac{M v_{1}^{2}}{2} + \frac{M^{2}}{4 m_{1}} (v_{2}^{2} + v_{1}^{2}) = E_{10} - M (\frac{E_{10}}{m_{1}}) + \frac{M^{2}}{2 m_{1}} (\frac{E_{10}}{m_{1}} + \frac{E_{20}}{m_{2}})$ (12)

$< E_{2} > = E_{20} - \frac{M v_{2}^{2}}{2} + \frac{M^{2}}{4 m_{2}} (v_{2}^{2} + v_{1}^{2}) = E_{20} - M (\frac{E_{20}}{m_{2}}) + \frac{M^{2}}{2 m_{2}} (\frac{E_{10}}{m_{1}} + \frac{E_{20}}{m_{2}})$ (13)

Summary of Average Energy Results for m₁=m₂=m

When m₁=m₂=m so that M=m the results for average E, <E> , are easily seen from equations 12 and 13 to be:

$< E_{1} > = \frac{E_{10} + E_{20}}{2} = < E_{2} >$ (14)

With a little more difficulty the results for the variances of E, <ΔΕ>, are given by the following equations:

$\begin{array}{l} < Δ E_{1} > = \frac{E_{10} + E_{20}}{4} = < Δ E_{2} > w h e n E_{10} = E_{20} \\ < Δ E_{1} > = \sqrt{2} \frac{E_{10} + E_{20}}{4} = < Δ E_{2} > w h e n E_{10} = 0 o r E_{20} = 0 \end{array}$ (15)

Discussion of Scattering for Equal Mass Atoms.

So, what really happens when the masses are equal, is that the energies redistribute themselves into a gaussian-like pattern with the gaussian width greater when the energy differences are greater. Of course, the minimum outcome for any energy is always zero, so the distribution tends to become biased toward its E=0 end.

If we start with mono-energetic atoms, E₀, so that E_total=2E₀, then the first variance will always be 0.250E₀. A fraction of these scattered atoms will have energy 2E₀ and an exactly equal fraction will have zero energy. The next scattering, when with atoms with energies E₀, can result in energies from zero energy up to 3E₀. When the next scattering is between 2 atoms that have energy of 2E₀ the final energy can be as large as 4E₀ but that is a very unlikely event. Of course, since neither is moving, atoms with zero energy don't scatter with other atoms of zero energy so these latter remain at zero energy. In fact the number of scatterings per second depends on the energy of the atoms, so this makes all the lower energy atoms less likely to scatter with similar low energy atoms.

We could write the following approximate differential equation for the rate of scattering of atoms

$\frac{d N}{d t} = n σ v_{r} \propto n σ \sqrt{\frac{2 E_{1}}{m_{1}} + \frac{2 E_{2}}{m_{2}}}$

where n is the atom density, v_r is some average relative speed, and σ is the collision cross section. Thus the rate of change of energies via scattering depends on the sum of the velocities of the two atoms involved. This is one of the mechanisms that I think would cancel out the usual tendency for the atoms to form a symmetric gaussian distribution centered at the average energy. The other mechanism is that, while any energy higher than the average energy is possible, the minimum energy is always zero so a lot of atoms tend to accumulate near the zero end of the number Vs energy distribution.

We can also say that there are few high energy atoms because they scatter quite often so that they usually get their energies degraded by scattering with lower energy atoms and become "thermalized".