Animation of Pulleys and Belt Drive System

Introduction

This animation provides learning of drive speed ratios and the dynamics of how the driven load affects the driving belt's sag. Its design algorithms also show how to maintain digital integrity of the links of the belt without slippage on the pulleys.

Figures

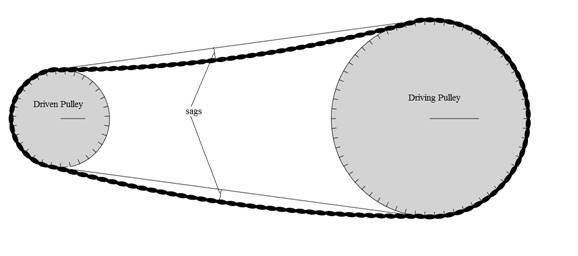
Figure 1. Pulleys with belt under motionless conditions.

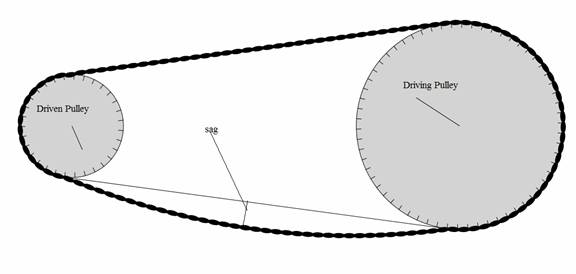
Figure 2. Pulleys with belt under driving conditions. Note the lack of sag on the belt's top span and the doubling of sag on the belt's bottom span.

Math

1. Initial Layout:

We will make integer numbers of equal length links on both free spans and on both pulleys by adjusting start angles on the left and right pulleys and by adjusting the horizontal distance between the pulleys. In order to get integer numbers of links on the pulleys we use the following algorithm:

$\begin{array}{l} n_{b} = int [(π - 2 θ_{b}) \frac{a_{b}}{l}] \\ n_{s} = int [(π - 2 θ_{s}) \frac{a_{s}}{l}] \end{array}$

(1.1)

where l is the link length, a_b is the radius of the big pulley and a_s is the radius of the small pulley.

Then we solve the equations (1.1) for θ_b and θ_s:

$\begin{array}{l} θ_{b} = π / 2 - n_{b} l / (2 a_{b}) \\ θ_{s} = π / 2 - n_{s} l / (2 a_{s}) \end{array}$

(1.2)

The math for the span between pulleys involves a quadratic equation:

$\begin{array}{l} δ r_{x} = a_{b} \sin (θ_{b}) - a_{s} \sin (θ_{s}) \\ δ r_{y} = a_{b} c o s (θ_{b}) - a_{s} c o s (θ_{s}) \\ δ x_{p} = δ r_{x} + \sqrt{{(n_{s p} l)}^{2} - {(δ r_{y})}^{2}} \end{array}$

(1.3)

where δx_p is the horizontal distance from the center of the small pulley to the center of the big pulley and n_sp is the previously chosen number of links in the free spans.

2. Motion:

Here the idea is to save a copy of the stationary belt and then have the moving belt segment morph gradually into the stationary segment as it arrives there. In order to achieve this, it is simpler to save several iterations of each link position in an array so that the link can be stepped sequentially to an exact and repetitive position.

The code to move a single segment along the belt path is shown below where i represents the integral link step number, n is the total number of links, m is the number of the current link being advanced, j is the discrete step number and there are njs steps for each full link advancement.

//i is the current value of advancement;

int k= i % n;

//advance all ellipses by len/njs from their stored positions

for(int m=0;m<n;m++)

{//m is the link number being advanced

int kmMod=(k+m) % n;

ellipse em=eList[m];

int index=njs*kmMod+j % njs;//2D data array, pA, index

em.x=pA[index][0];

em.y=pA[index][1];

em.angle=pA[index][2];

}

j++;

if(j % njs==0) i++;