Computing the ray trace for a thin lens

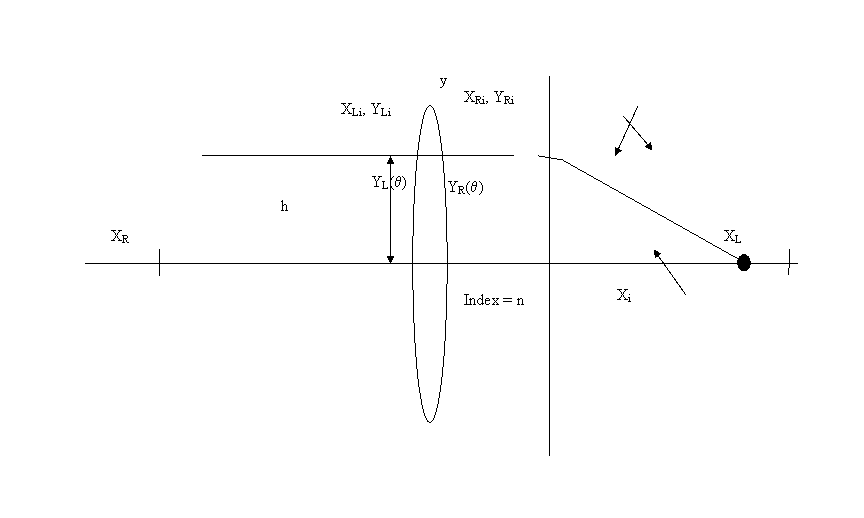
To compute the refracted rays we first have to define the centers of curvature of the left (L) and the right (R) surface of the lens. In terms of the diameter (D) of the lens, the maximum angles are:

;

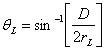and this results in the following distances to the centers for curvature:

Then the following are the x coordinates of the left and right surfaces of the lens:

;

The angle of interception of the ray at height h relative to the normal of the left surface of the lens is:

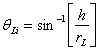
And this results in the following x and y coordinates for the point of interception:

The angle of refraction at the left surface is given by Snell’s law as:

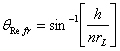
and this results in the following slope relative to the x axis for the refracted ray:

, a negative number

and the following equation for the y coordinate Vs x for the refracted ray

An additional equation for the y coordinate of the right surface of the lens is:

To compute the x intercept of the refracted ray with the lens right surface we set the squares of these two equations equal:

Solution for the x intercept on the right surface of the lens is then given by:

and similarly:

The angle (relative to the x axis) at y_Ri of the right surface normal is given by:

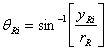, a positive number

And as stated above the angle of the refracted ray relative to the x axis is:

, a negative number

and thus the incident angle relative to the normal is:

The angle of refraction (relative to this surface normal) is then given by:

The angle of this second refracted ray relative to the x axis is then given by:

, a negative number.

The equation for intercept of the second refracted ray with the x axis is:

where

, again a negative number.

Then the x intercept occurs at: