Equations for refraction at a planar interface between 2 media.

Assume a wave in incident medium 1 of the form:

where

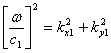
c₁ is the speed of the wave fronts and w is their radian frequency.

Similarly consider a wave in medium 2 of the form

where

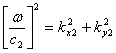
At the interface between the two media, the wave fronts must be continuous even though c₁ is not equal to c₂. In order to achieve this continuity of the wavefronts k_y2 must be equal to k_y1. Then the equations are:

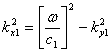
The sines of the propagation angles with respect to the normal are:

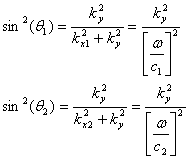
But we know that c₁ is related to c₂ by the simple relation

where c is the speed of light in vacuum and n_i are the indices of refraction of the 2 media.

Therefore the equations for sin(q) simplify to

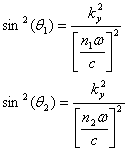
and from these equations we can deduce:

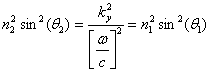
which is called Snell’s law.