Refraction and Reflection in two Media Layers
Figures
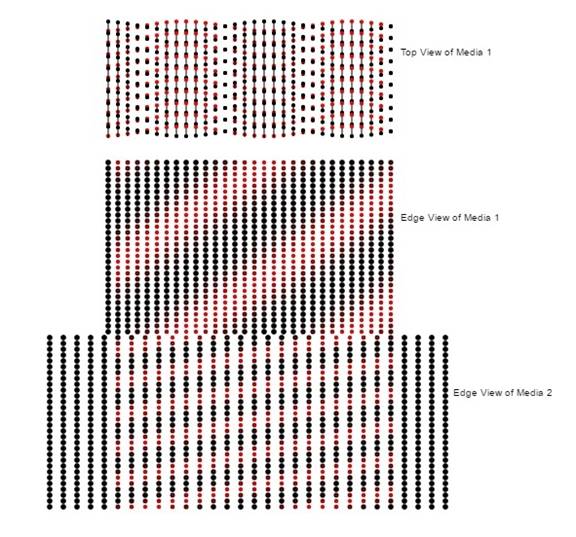
Figure 1: Refraction only. Top view and edge view of the dipoles in two transparent media with an S polarized electromagnetic (em) wave incident on the top media. With s polarization, in edge view, you will see only the red (positive) or the black (negative) end of the dipole and these will oscillate at the frequency of the em wave. In the edge views, note the continuity of the wave phase at the interface between the two media. This is a more accurate way of showing how Snell's law is obeyed. The usual way is that the tangential component of the wave vector is the same on both sides of the interface. In the top view, the bottom edge of the top view is coincident with the near top corner of the edge view. So the colors at the bottom edge of the top view should agree with the color of the top edge of the edge view as is the case.
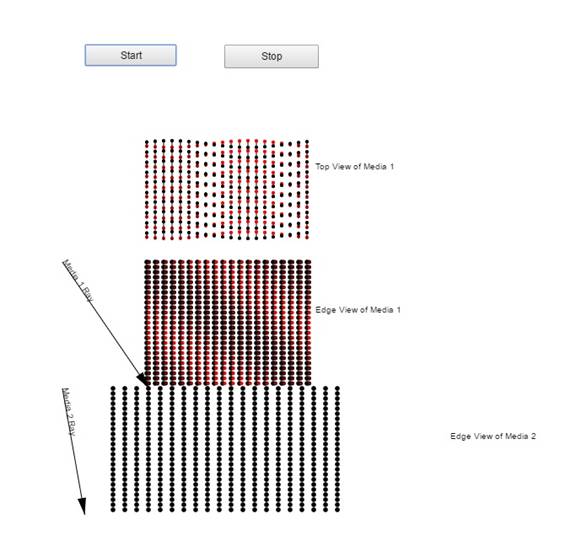
Figure 1: Reflection only. Top view and edge view of the dipoles in the top transparent media with an S polarized electromagnetic (em) wave incident on it. With s polarization, in edge view, you will see only the red (positive) or the black (negative) end of the dipole and these will oscillate at the frequency of the em wave. The polarization due to the reflected wave moves upward and to the right according to the phase equation 1 given below. The refracted wave in media 2 is not shown here.
The equation for the reflected polarization is
|
|
(1) |
where w is the radian frequency, kx is the horizontal component of the wave vector and ky is the vertical component of the wave vector and h1 is the thickness of layer 1.
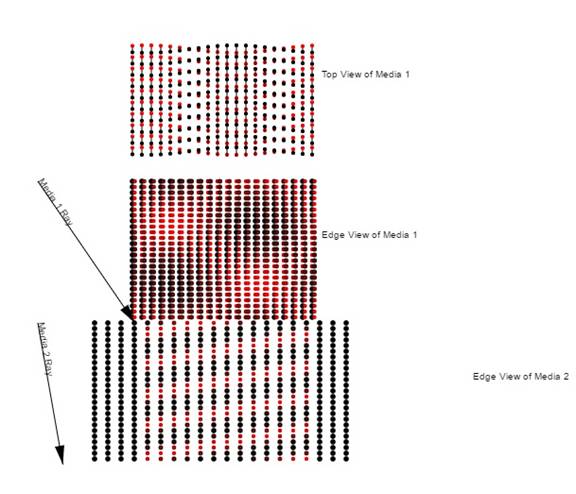
Figure 1: Refraction and Reflection. Top view and edge view of the dipoles in two transparent media with an S polarized electromagnetic (em) wave incident on the top media. With s polarization, in edge view, you will see only the red (positive) or the black (negative) end of the dipole and these will oscillate at the frequency of the em wave. In the edge views, note the continuity of the wave phase at the interface between the two media. This is a more accurate way of showing how Snell's law is obeyed. The usual way is that the tangential component of the wave vector is the same on both sides of the interface. In the top view, the bottom edge of the top view is coincident with the near top corner of the edge view. So the colors at the bottom edge of the top view should agree with the color of the top edge of the edge view as is the case.
When reflection from the interface between the media is included, we will have a wave that moves upward and to the right as time proceeds. Also, the amplitudes of the waves in both media are affected by the transmission and reflection coefficients. The amplitude effects can be seen by changing the value of n2 between its extremes.