Derivation of the equations of special relativity
The requirements are:
- The relationship between giving the scaling of time and space measurements in differently moving systems shall be linear (e.g. x=ax+bt and t=dt+ex where a, b, d and e do not depend on x or t) in order to avoid making a given system special.
- For special relativity, the relative speeds must be constant.
- Observers making measurements of c, the speed of light, in all systems in vacuum will get the same result.
- It will never be possible by any physical measurements to establish a fundamental difference between 2 systems.
It will be sufficient for this derivation to have relative motion between only the x axes of the 2 systems. That means that the following equations will be true for the y and z dimensions:
![]()
where the primed system is herein considered by the unprimed system to be moving at speed v and the unprimed system is considered by the primed system to be moving at speed v, thus establishing perfect anti-symmetry between the systems.
Then, because of the linearity requirement 1 and the no difference requirement 4 we have the following relationships between x and x.
![]() (1)
(1)
Now we must determine if there is any difference between the 2 linear factors g and g.
We make measurements, from the unprimed system of the length of a ruler of length L in the primed system. Letting t=0 in both systems, and setting
![]()
we find that the corresponding x values are x=L/g and x=L/g and these values of x must be equal to satisfy requirement 4. That means that g=g.
To determine g, we make use of requirement 3. Let a light pulse be emitted at x=x=0 and arrive at points x and x on the x axes at times t and t so that x=ct and x=ct. Then substituting these values into equation 1 we have:
![]() (2)
(2)
Solving equations 2 for g we have:
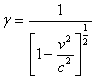 (3)
(3)
Using g in equations 1 we obtain:
![]() (4)
(4)
![]() (5)
(5)
These equations alone, via the factor g, would appear to quantify the differences in aging in the famous Twin Paradox. However, the real paradox is that the same factor applies equally to the unprimed quantities that we can derive from equations 4 and 5 and obviously we cannot have both the traveling twin and the one that stays home remain younger. Reference 1 does a reasonably good job of explaining that the real asymmetry between the world paths of the two twins is the accelerations of the traveling twin.[1]