Computing the reflection angle of a ray at a given height and angle to a spherical mirror:

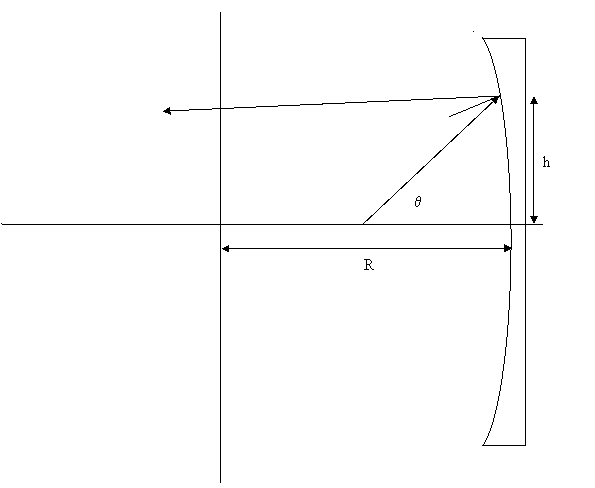
At height h the angle with respect to the x axis of the surface normal is

where R is the radius of curvature of the mirror.

The angle of incidence of the ray with respect to the normal is then

and, of course, the angle of exitance with respect to the normal is the same as that angle of incidence.

That makes the angle of exitance with respect to the x axis:

i.e. the ray would be exiting upward at angle q if the mirror had no curvature and downward at angle -q if q = q _nx .

For confined rays, q _e will be negative for positive h.

The y height of the exiting ray is given by:

where x is assumed to be positive going to the right and

with x=0 at the center of curvature of the mirror.

In general we want to compute the (x,y) intersection of an arbitrary ray with the mirror surface. That surface is given by

and the ray can be described by the equation

We wish to find x for which these y’s are the same.

and of course: