Computing the reflection angle of a ray at a given height and angle to a spherical mirror:
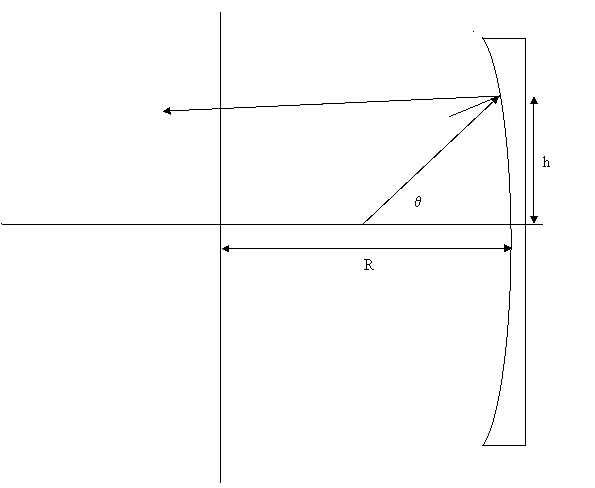
At height h the angle with respect to the x axis of the surface normal is
![]()
where R is the radius of curvature of the mirror.
The angle of incidence of the ray with respect to the normal is then
![]()
and, of course, the angle of exitance with respect to the normal is the same as that angle of incidence.
That makes the angle of exitance with respect to the x axis:
![]()
i.e. the ray would be exiting upward at angle q if the mirror had no curvature and downward at angle -q if q = q nx .
For confined rays, q e will be negative for positive h.
The y height of the exiting ray is given by:
![]()
where x is assumed to be positive going to the right and
![]()
with x=0 at the center of curvature of the mirror.
In general we want to compute the (x,y) intersection of an arbitrary ray with the mirror surface. That surface is given by
![]()
and the ray can be described by the equation
![]()
We wish to find x for which these y’s are the same.
![]()
and of course:
![]()