Lumped Resonator Math
Introduction
This will be a summary of the mathematics used to compute the lumped reflectors, the Reflectance, R, the Transmittance, T, and the energy density U(z) in a lumped resonator. The idea of a lumped resonator is that it gives the viewer the option of both the reflectance and position of the reflecting elements. The reflectance is then provided by choosing a ¼ wave thickness layer (at the nominal wavelength) of appropriate index of refraction. The thickness and index of the reflecting elements are then included in the calculation of R, T, and U(z).
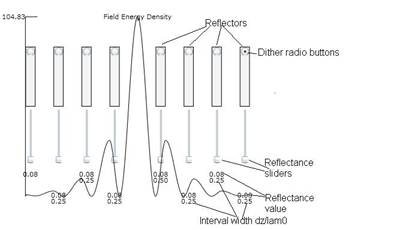
Figure 1: Showing some of the viewer adjustable
elements in the animation. The tall
rectangles are the individual reflectors whose spacings can be changed by
dragging with the mouse and whose reflectances can be varied by the sliders
beneath them.
Setup of reflecting elements
For a ¼ wave thick layer of index of refraction, nH, the intensity reflection coefficient is
![]() (1)
(1)
where nA is the index of the ambient medium wherein nH is immersed. By choosing nH>>nA we can make R indefinitely large. The thickness of the reflector layer is then:
![]() (2)
(2)
So we just insert these ¼ wave layers in between the intervals, dzi, of the resonator.
Calculation of R at T of the Entire Resonator
To make this calculation we use a combination of interface matrices, I, and phase matrices, P. The interface matrix is:
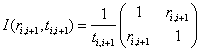 (3)
(3)
where
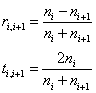 (4)
(4)
and ni is the index of the ith medium while ni+1 is the index of the medium that is toward the substrate side of the ith medium.
The phase matrix, which transforms the field from the right side of the layer to the left side, for the ith layer is:

where hi is the thickness of the ith layer.
To obtain the overall reflection coefficient, rT and transmission coefficient, tT, These matrices are multiplied together as shown below:
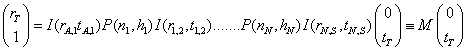 (5)
(5)
where there are N layers and the subscript A denotes the
incident medium and S denotes the substrate medium and the 1 in vector on the
left side denotes unity input.
Using the terms of M in equation 5 we have:
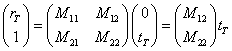 (6)
(6)
which results in the following equations for rT
and tT
![]() (7)
(7)
so that:
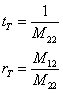 (8)
(8)
The values of rT and tT are generally complex and we need to take the absolute values squared for the intensity ratios, R and T:
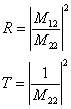 (9)
(9)
Energy Density U(z)
The computation of the electric fields Vs depth, z, in the
resonator follows similar lines to that of R and T. To be definite, assume that the field is
incident from the left side and that z increases going to the right toward the
substrate. The same matrices are used except, this time,
the P(ni, hi) becomes P(ni, hi-z)
since we need to transform the known transmitted field at the right side of the
resonator backwards to the left side of the resonator. Using this expression for P. we will have z=h
at the right side of the layer and z=0 at the left side of the layer.
Thus the expression for the fields in the rightmost layer is
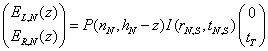 (10)
(10)
where z ranges from hN to 0 so that when z=hN
we are at the right hand side of the layer and when z=0 we are at the left hand
side of the layer.
Similarly, the expression for the fields in the N-1 layer are:
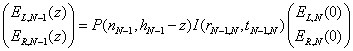 (11)
(11)
and this process continues to layer 1. Naturally, we need to keep track of the total value of z and this is done by maintaining a list:
![]() (13)
(13)
where zj are the z’s inside the Nth layer and Zj is the global collection of depth values that will be completed after all the fields in layer 1 are computed.
Having obtained the field vector in, say, the mth layer, we do the following to compute the field energy density:
![]() (14)
(14)
To perform the above operations efficiently using a computer
we iterate as follows. First form the value of EL,N at the right
hand side of the Nth layer:
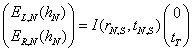 (15)
(15)
Then successively iterate this E field value through the set of Nth layer zs, from hN to 0:
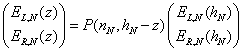 (16)
(16)
Next multiply the result for the final z by the appropriate interface matrix:
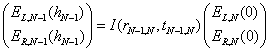 (17)
(17)
Then repeat the iteration in equation 16 for its range of z values:
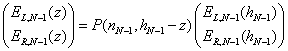 (18)
(18)
The above algorithm avoids the need for most of the 2x2 matrix multiplications that would be needed if we used equation 11.
Phasors for visual representation of the reflection process
In order to make the above calculations more intuitive, we can choose to present a visual representation in the complex plane of the contributions to reflectance of each of the interfaces of the resonator. These contributions are called phasors. This will not be an exact representation because we won’t include multiple reflections in each layer. For the Nth interface contribution, the calculation starts off as in equation 15:
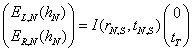
Then the left-going field in the Nth interval is then just:
![]() (19)
(19)
We wish to observe the effect of this component at the left-hand boundary of the resonator. To do that, we must appropriately shift the phase of this component. This involves multiplying by the set of phase factors in the (1,1) elements of the P matrix:
This product becomes:
![]() (20)
(20)
where the superscript 0 indicates that EL,N has
been transformed to the left side of the resonator.
For the (N-1,N) interface we find its left going component by a calculation like equation 17
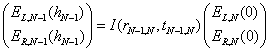 (21)
(21)
so that
![]() (22)
(22)
Then we make a similar multiplication by the phase factors as in equation 20:
![]() (23)
(23)
and so on for the remainder of the interfaces. The result of such a phasor representation is shown in Figure 2:
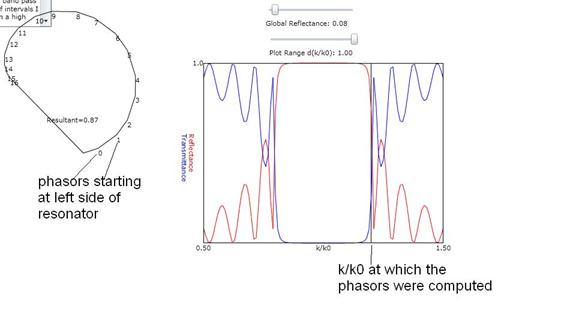
Figure 2: Phasors for a resonator with 8
intervals. There are 17 phasors corresponding
to the 16 interfaces numbered 0-16 starting from the left side of the
resonator. The k/k0 value for the
phasors is shown by the vertical line cursor in the Reflectance/Transmittance
plot.