Ring Resonator Interferometer Dynamics

Introduction

Ring resonators operating in non-steady state mode can be useful. This document will detail how ring resonators fields are built up and how they dissipate.

Math for Maximum Resonance

To keep this as simple as possible we will let only one mirror have non-zero transmission so that this mirror will be both the input and output mirror. That mirror's amplitude reflectance as observed from outside the resonator will be labeled r_e and that from inside the resonator will be r_i. For our purposes we will assume that r_i is a positive real number. Optical physics then dictate that r_e will be -r_i. To get started let us assume that the total optical path around the resonator is an integer number, N, of wavelengths so that the phase delay of light around the resonator is $2 π N$ .

For our purposes it will be adequate to measure time in units of L/c where L is the resonator path length and c is the speed of light. For L=30 cm L/c is 1 nanosecond which is an experimentally convenient to measure time increment.

Light that is being injected n units after the source has started up, will be coherently reinforced by the echoes of its preceding injections by the quantity:

$F (n) = \sum_{k = 0}^{k = n - 1} r_{i}^{k}$

(1.1)

It is well known that this is a geometric series and has the exact sum:

$F (n) = \frac{1 - r_{i}^{n}}{1 - r_{i}}$

(1.2)

Now, if the source provides amplitude E₀, the primitive input through the mirrors transmission coefficient will be

$e_{0} = t E_{0}$

(1.3)

and, at any time n after the source has been started, this e₀ will be enhanced to e_n by factor F(n):

$e_{n} = t E_{0} F (n) = t E_{0} \frac{1 - r_{i}^{n}}{1 - r_{i}}$

(1.4)

Now we can express t as a function of r_i:

$t = \sqrt{1 - r_{i}^{2}}$

(1.5)

Since the resonator has no internal loss, it would be reasonable to expect that, during steady state operation, the sum of the transmitted intensity out of the input mirror and the reflected intensity from the input mirror will be just E₀. We will now show that to be true. Note that

$e_{n t r a n s m i t t e d} = t^{2} E_{0} \frac{1 - r_{i}^{n}}{1 - r_{i}} = (1 - r_{i}^{2}) E_{0} \frac{1 - r_{i}^{n}}{1 - r_{i}} = E_{0} (1 + r_{i}) (1 - r_{i}^{n})$

(1.6)

However the reflected field is always:

$e_{r e f l e c t e d} = r_{e} E_{0} = - r_{i} E_{0}$

(1.7)

Steady state means that n in equation (1.6) goes to infinity so that e_transmittedbecomes:

$e_{s s - t r a n s m i t t e d} = E_{0} (1 + r_{i})$

(1.8)

Then, combining equations (1.7) and (1.8) we have

$e_{s s - t r a n s m i t t e d} + e_{r e f l e c t e d} = E_{0} (1 + r_{i}) - E_{0} r_{i} = E_{0}$

(1.9)

as expected.

The output Vs time after the input has started is proportional will look like an exponential due to the 1-r^n term. Below is a plot Vs n:

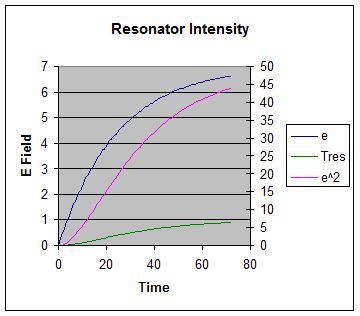
Figure 1. Plots of the internal field and intensity as well as the resonator output Vs the integer n which represents time for an amplitude reflectance of 0.96.

The curve for e in Figure 1 looks like the exponential:

$f (n) = [1 - e x p (- \frac{n}{n_{e}})]$

(1.10)

where n_eis a constant that defines the value of n when f(n)= 1-1/e.

Note that the term in the numerator of equation (1.4)

$1 - r^{n} = 1 - \exp (n \ln (r))$

(1.11)

is an identity which can be confirmed by taking the logarithm of both sides of the equation:

$n \ln (r) = \ln (\exp (n \ln (r))$

(1.12)

so that

$n_{e} = - \frac{1}{\ln (r)}$

(1.13)

Thus we can conveniently compute the values or rⁿ by computing a natural logarithm and a single exponential.

Math when off Resonance

When the path length around the resonator is increased so that the total phase shift is

$Δ ϕ = 2 π N + δ$

(1.14)

then equation (1.1) becomes:

$F_{o} (n) = \sum_{k = 0}^{k = n - 1} r_{i}^{k} e^{i k δ}$

(1.15)

and equation (1.2) becomes:

$F_{o} (n) = \frac{1 - r_{i}^{n} e^{i n δ}}{1 - r_{i} e^{i δ}}$

(1.16)

The numerator in equation (1.16) still goes to zero as n becomes very large. But the denominator in equation (1.16) is quite different from the denominator in equation (1.2)

We can see how this effects the resulting e_n by multiplying by the complex conjugate:

$F_{o} (n) = \frac{1 - r_{i}^{n} e^{i n δ} [1 - r_{i} e^{- i δ}]}{(1 - r_{i} e^{i δ}) (1 - r_{i} e^{- i δ})} = \frac{(1 - r_{i}^{n} e^{i n δ}) (1 - r_{i} e^{- i δ})}{1 - 2 r_{i} \cos δ + r_{i}^{2}}$

(1.17)

When n goes to infinity, the minimum value of the F_o in equation (1.17) is 1/(1+r²) and the maximum value is 1/(1-r).

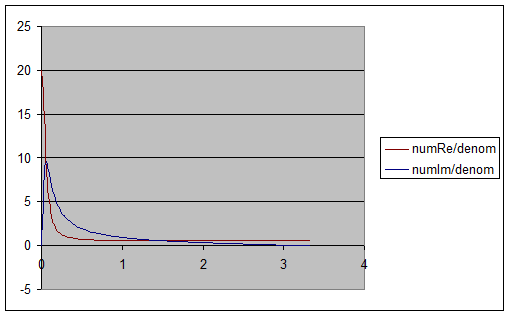
Figure 2:Real and Imaginary parts of the field amplitude (when fully charged) Vs phase offset expressed in radians.

Discharge of Amplitude and Intensity

To express the amplitude Vs n when discharging we first look at the expression for charging in equation (1.10)

$f (n) = [1 - e x p (- \frac{n}{n_{e}})]$

(1.18)

Discharging the amplitude has the same time constant as charging and thus

$f_{d} (n) = \exp (- \frac{n - n_{0}}{n_{e}})$

(1.19)

where f_d(n) is the field amplitude at pass n, n is still the total number of passes after turn-on of the input and n₀ is the number passes at which the input was turned off. Since f_d is the field, the intensity, I, must be proportional to this quantity squared:

$I_{d} (n) = \exp (- 2 \frac{n - n_{0}}{n_{e}})$

(1.20)

Recall from equation (1.13) that

$n_{e} = - \frac{1}{\ln (r)}$

(1.21)

For this section let me generalize the definition of r to be the coefficient of the single pass amplitude return to its starting point. Then $r^{2}$ will be the coefficient of the single pass intensity return to its starting point. These coefficients will then be reduced by mirror scattering losses, mirror absorption losses, and bulk absorption losses of any media between the mirrors.

Now let's relate n_e to the intensity losses per pass which are expressed:

$l_{I} = 1 - r^{2} = (1 + r) (1 - r)$

(1.22)

Now we will specialize the intensity losses to the case where 1-r<<1 so that

$l_{I} \approx 2 (1 - r)$

(1.23)

Solving this equation for r we have:

$r \approx 1 - \frac{l_{I}}{2}$

(1.24)

Thus we have

$n_{e} \approx - \frac{1}{\ln (1 - l_{I} / 2)}$

(1.25)

Since l_I<<1 it is a good approximation to say

$\ln (1 - \frac{l_{I}}{2}) \approx - \frac{l_{I}}{2}$

(1.26)

and therefore

$n_{e} \approx \frac{2}{l_{I}}$

(1.27)

Then equation (1.20) becomes

$I_{d} (n) = \exp (- 2 \frac{n - n_{0}}{n_{e}}) = \exp (- 2 \frac{n - n_{0}}{\frac{2}{l_{I}}}) = \exp (- l_{I} (n - n_{0}))$

(1.28)

I wish to point out that equation (1.28) is correct and is in agreement with published results for "cavity ring-down spectroscopy".

Figure 3:Charge and discharge of a resonator's amplitude and intensity as a function of the number of passes since starting.

Note in Figure 3 that the amplitude discharge is the complement of the amplitude charge. Also note that this is not the case for the intensity discharge which is far faster than the intensity charge. This latter asymmetry is true of the energy of capacitors in series RC circuits as well.