Acceleration of a Mass by Gas Expansion

Calculations

The equation for the speed, v, of the mass as a function of the volume parameter, h, is:

$v^{2} = \frac{2}{m} (U_{0} - U) = \frac{2 U_{0}}{m} (1 - \frac{h_{0}}{h})$

where m is the mass, U₀ is the starting internal energy, h₀, is the starting boundary of the gas, and h is the present boundary of the gas. Now we recognize that v=dh/dt so that equation (1.1) can be re-written:

$\frac{d h}{d t} = \sqrt{\frac{2 U_{0}}{m}} \sqrt{1 - \frac{h_{0}}{h}}$

(1.2)

Again we can re-write equation (1.2) by keeping all h terms on the left side of the equation:

$\frac{d h}{\sqrt{1 - \frac{h_{0}}{h}}} = \sqrt{\frac{2 U_{0}}{m}} d t$

(1.3)

Now we would like to integrate both sides of this equation. To do this for the left side we first make the change of variable u=h₀/h. Then

$\begin{array}{l} d u = - \frac{h_{0} d h}{h^{2}} \\ d h = - \frac{h^{2}}{h_{0}} d u = - \frac{h_{0}}{u^{2}} d u \end{array}$

(1.4)

Converting the left hand side of equation (1.3) to be variable in u we have:

$- h_{0} \frac{d u}{u^{2} \sqrt{1 - u}} = \sqrt{\frac{2 U_{0}}{m}} d t$

(1.5)

The integration of the right side of equation (1.5) is trivial and the integral of the left side can be found in tables:

$\int \frac{d u}{u^{2} \sqrt{1 - u}} = \frac{\sqrt{1 - u} + u \tanh^{- 1} \sqrt{1 - u}}{u} = - \frac{1}{h_{0}} \sqrt{\frac{2 U_{0}}{m}} t$

(1.6)

The u integral in equation (1.6) has upper limit u=1 and lower limit u=h₀/h where h>h₀. At its upper limit the result is zero. Equation 6 can be solved for the time, t, as a function of u:

$t = h_{0} \sqrt{\frac{m}{2 U_{0}}} \frac{\sqrt{1 - u} + u \tanh^{- 1} \sqrt{1 - u}}{u}$

(1.7)

If we change h in uniform increments and compute the change of time at these values of h, we can obtain dh/dt which is the speed of the mass. To start let's re-write equation (1.7) in terms of h:

$t (h) = h_{0} \sqrt{\frac{m}{2 U_{0}}} \frac{\sqrt{1 - \frac{h_{0}}{h}} + \frac{h_{0}}{h} \tanh^{- 1} \sqrt{1 - \frac{h_{0}}{h}}}{\frac{h_{0}}{h}} \equiv h_{0} \frac{f (h)}{v_{\max}}$

(1.8)

where I have defined v_max as the square root of 2U₀/m which is the maximum speed that can be achieved. Then speed is defined as:

$\frac{d h}{d t} = \frac{v_{\max}}{h_{0}} \frac{h_{i + 1} - h_{i}}{f (h_{i + 1}) - f (h_{i})}$

(1.9)

Figure

time

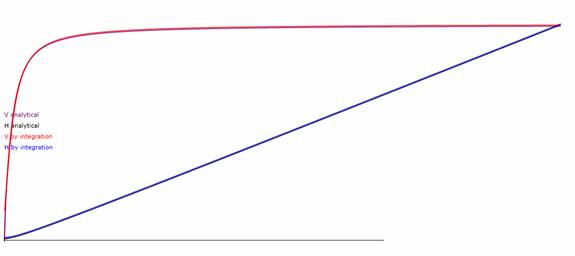
Plot of the mass speed V (red and purple) and position H (black and blue) versus time. The results are by numerical integration and calculus integration, respectively.