Cylinder on an Inclined Plane

Introduction

The acceleration of a cylinder that rolls on an inclined plane is generally considerably less than that of a similar mass that slides without friction on the same plane. The reason for this difference is that rolling mass has more inertia than the sliding mass due to the need to accelerate both its rolling speed and its center of mass motion. This animation will allow the viewer to see the variation of the acceleration due to changing the mass distribution of the cylinder.

Figures

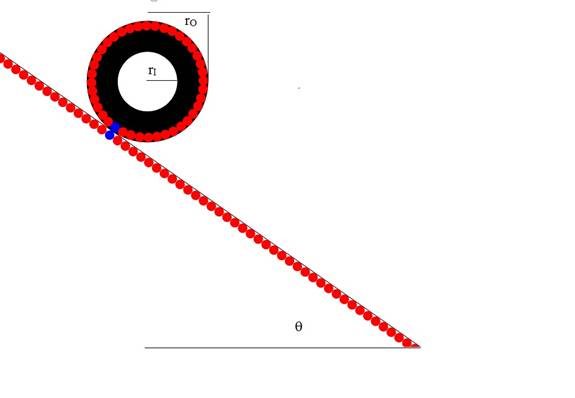
Figure 1. Cylinder rolling on a plane inclined at angle θ from the horizontal. Inner and outer radius are labeled.

Physics of Rolling Cylinder

The cylinder is accelerated angularly by application of a force, F, at the point of contact on the plane. The force results in a torque, T, about the center of mass of the cylinder. The torque is defined as:

$T = r \times F$

(1.1)

where r is the radius of the cylinder and the x symbol denotes cross product.

Since the mass rolls without slipping, its center of mass moves at speed

$v = ω r$

(1.2)

where ω is the angular rate of rotation (radians sec^-1).

The cylinder center of mass (its axis) is accelerated at the rate:

$\frac{d v}{d t} = \dot{ω} r$

(1.3)

where the dot over the ω denotes time derivative.

Even if there were no center of mass motion, all of the masses in the cylinder also have to be accelerated and rotate at ω. The inertia (i.e. resistance to rotation) of these depend on their radial location. The relation between rotational acceleration and applied torque obeys the following equation:

$I \dot{ω} = | r \times F |$

(1.4)

where the angular moment of inertial, I, is defined as (see Appendix below):

$I = \int_{R_{I}}^{R_{O}} r^{2} d m (r)$

(1.5)

where R_I, R_O are the inner and outer radius and dm(r) is the incremental mass at radius r. For a cylinder dm(r) is defined as

$d m (r) = 2 π L ρ r d r$

(1.6)

where ρ is the mass per unit volume and L is the axial length of the cylinder.

Inserting equation (1.6) into equation (1.5) and integrating over r we obtain:

$I = \frac{2 π}{4} ρ L (R_{O}^{4} - R_{I}^{4})$

(1.7)

By performing a similar integral we obtain the total mass of the cylinder:

$M = \int_{R_{I}}^{R_{O}} d m (r) = 2 π L ρ \int_{R_{I}}^{R_{O}} r d r = \frac{2 π}{2} L ρ (R_{O}^{2} - R_{I}^{2})$

(1.8)

Dividing equation (1.7) by equation (1.8) we obtain the simplified result:

$I = \frac{M}{2} (R_{O}^{2} + R_{I}^{2})$

(1.9)

It should be noted that equation (1.9) is valid only for cases where the density, ρ, remains constant between R_I and R_O. Note that I can vary from MR_O²/2 (solid cylinder) to MR_O² (hoop) as r_I varies from 0 to r_O.

In addition to the angular inertia, we have to include the inertia associated with the center of mass's motion. That component is

$I_{C M} = M r_{O}^{2}$

(1.10)

Then the total inertial moment is:

$I_{t o t a l} = \frac{M}{2} (3 r_{O}^{2} + r_{I}^{2})$

(1.11)

Note that I_total can vary from 3MR_O²/2 (solid cylinder) to 2MR_O² (hoop) as r_I varies from 0 to r_O.

We should also compute the torque available due to an inclined plane. If the plane's angle with the horizontal is θ then the torque is

$T = M g r_{O} \sin θ$

(1.12)

where g is the acceleration of gravity.

Then the angular acceleration is

$\dot{ω} = \frac{M g r_{O} \sin θ}{I_{t o t a l}} = \frac{2 g r_{O} \sin θ}{(3 r_{O}^{2} + r_{I}^{2})}$

(1.13)

On many machines, the rolling mass is connected to a much larger non-rolling mass. An example would be the wheel on a bicycle. One might consider the question of the effect on acceleration of adding/removing mass to/from the rolling part as compared to a similar effect on the non-rolling part. Looking at equation (1.11), if the mass is added or removed near r_O of the roller so that r_Iis approximately equal to r_O , then its effect on inertia is twice as much as if the mass is added or removed from the non-rolling part i.e.:

$\begin{array}{l} \frac{δ I_{t o t a l}}{δ M} \approx \frac{1}{2} (3 r_{O}^{2} + r_{I}^{2}) \approx 2 r_{O}^{2} r o l l i n g \\ \frac{δ I_{n o n - r o l l i n g}}{δ M} \approx r_{O}^{2} n o n - r o l l i n g \end{array}$

(1.14)

Appendix: Torque required to accelerate the angular rate of a mass at radius r

It is well understand that the force required to linearly accelerate a mass follows Newton's law of motion:

$m \frac{d v}{d t} = F$

(1.15)

The force required to change the angular rate of a mass at radius r is then:

$m r \frac{d ω}{d t} = F$

(1.16)

Since we want to have the torque corresponding to this force we multiply both sides of the equation by the radius, r.

$m r^{2} \frac{d ω}{d t} = r F = T$

(1.17)

Equation (1.17) can be thought of as the reaction torque that resists applied torques of the opposite sense.