Rotor-Disc and Rotor-Rotor Collisions Inside a Box
Introduction
As a
prologue to seeing how increasing the number of degrees of motional freedom
leads to changes in the energy probability distribution function, the following
shows how the conservation laws are used to compute the effects of collisions
of the rotors and discs of the title.
This use of the conservation laws is fairly unusual and worth
studying.
Computation for Rotor and Disc Colliding
First consider the angular momentum of 2 linearly moving masses
For an arbitrary origin of position vectors, the angular momentum, L, is:
![]()
where m's are masses, r's are the position vectors and the v's are the velocity vectors. This expression, of course, depends on the origin of coordinates.
Now we consider the case of the axis of rotation (or origin) being the center of mass, rCM:
![]()
![]()
![]()
![]()
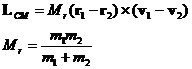
Note that, in the absence of a collision, LCM remains constant with time since the cross product of v with itself is zero.
![]()
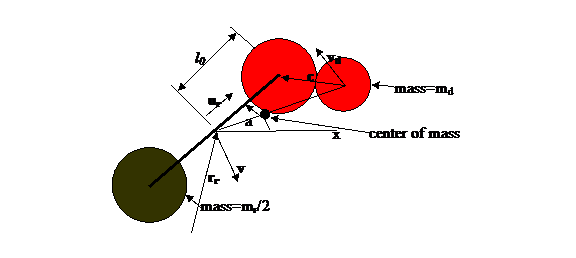
Figure 1: Illustration of rotor and a disc. The rotor rotational angle is a
and center of mass velocity v The distance between the centers of the
rotor end discs is 2l0 and the radius of the end discs is br while the single disc radius is bd Thus a collision is computed when the
distance between disc center and either rotor end center is less than br+bd
Linear momentum, p, is conserved during a collision.
![]()
Let dv=dv1, then
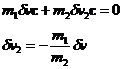
where c is a unit vector pointing from the center of the free disc to the center of the rotor end disc on which the collision is taking place. Let's specialize the masses so that m1=mr and m2=md where subscripts r and d correspond to rotor and free disc.
The angular momentum due to rotor's rotation is a combination of the angular momentum due to rotation of the 2 end discs about the axis and that due to rotation of each of the end discs about their own center. The moment of inertia due to the former rotation is ml02 and the moment of inertia due to the latter rotation is mbr2/2. For notational brevity we will define the following value for l as a combination of the two quantities in the moment of inertia:
![]()
If w is the rotation rate of the rotor, the total initial angular momentum is:
![]()
Final angular momentum is:
![]()
Setting final equal L to initial L we have
![]()
![]()
For simple discs, at the moment of collision, r1-r2 is parallel to c
so the cross product is zero. But, for a
disc-rotor collision, the CM of the rotor is not at the center of the end disc
so the change in angular momentum is finite.
![]()
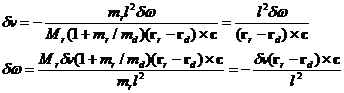
Using the expression for dw in the energy conservation equation below
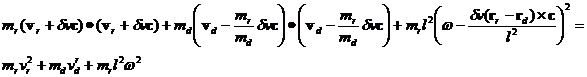 we
obtain the following expression for dv:
we
obtain the following expression for dv:
![]()
Computation for Two Rotor Collision.
Now let's consider what must be done to modify the above equation when we have two rotors rather than a rotor and a disc. The angular momentum associated with the linear motion of the rotors is the same as before:
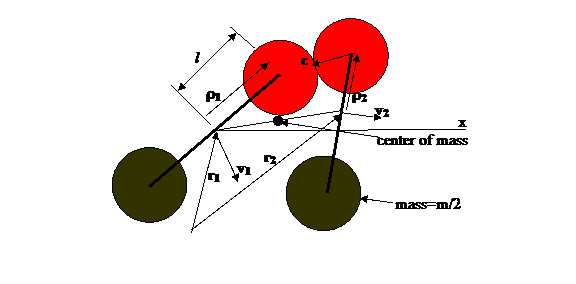
Figure 2: Illustration of 2 rotors colliding
. The distance between the
centers of the rotor end discs is 2l and the radius of the end discs is br Thus a collision is computed when the
distance between disc center and either rotor end center is less than 2br. r is the
vector from the axis of the rotor to the center of its colliding end disc, and c is a unit
vector along the line from the center of one rotor's end disc to the center of
the one of the end discs of the other rotor.
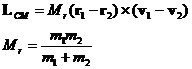
![]()
Let dv=dv1, then
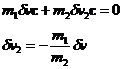
where now the r1 and r2 vectors point to the rotation axes of the rotors. However, when we define the conservation of angular momentum there are now two rotation rates, w, to consider.
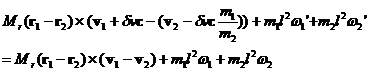
The collision of the rotors results in equal and opposite force impulses, Pc, to the rotor ends in question. We can convert these force impulses to torque impulses via the standard equation for torque:
![]()
where r is the vector from the axis of the rotor in question to the center of its colliding end disc. Note that the actual impulse point is at the radius of the end disc and therefore the vector, rP, to the impulse point is
![]()
and the torque impulse becomes
![]()
where we have taken into account the fact that c x c=0.
Then the values of the change in w of each of the rotors will be:
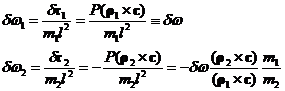
Then the conservation of L equation can be rewritten with
just one dw
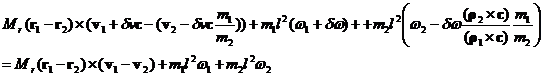
and this equation can be solved in for dw in terms of dv:
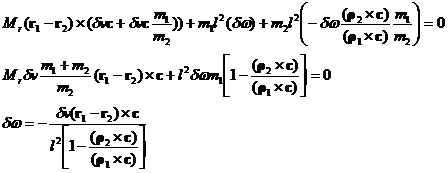
The energy equation is then
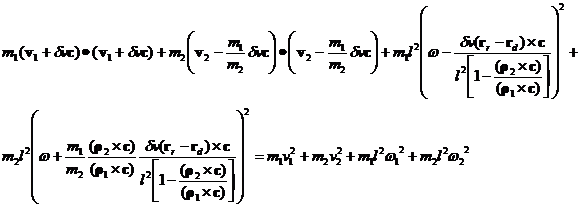
The result for dv is rather messy. To shorten the expression, define f as the following fraction:
![]()
Then:
![]()