Rotor-Disc and Rotor-Rotor Collisions Inside a Box

Introduction

As a prologue to seeing how increasing the number of degrees of motional freedom leads to changes in the energy probability distribution function, the following shows how the conservation laws are used to compute the effects of collisions of the rotors and discs of the title. This use of the conservation laws is fairly unusual and worth studying.

Computation for Rotor and Disc Colliding

First consider the angular momentum of 2 linearly moving masses

For an arbitrary origin of position vectors, the angular momentum, L, is:

where m's are masses, r's are the position vectors and the v's are the velocity vectors. This expression, of course, depends on the origin of coordinates.

Now we consider the case of the axis of rotation (or origin) being the center of mass, r_CM:

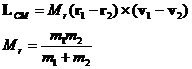
Note that, in the absence of a collision, L_CM remains constant with time since the cross product of v with itself is zero.

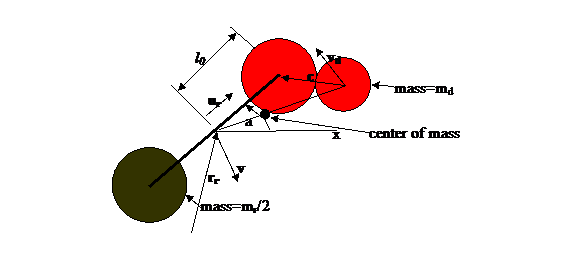
Figure 1: Illustration of rotor and a disc. The rotor rotational angle is a and center of mass velocity v The distance between the centers of the rotor end discs is 2l₀ and the radius of the end discs is b_r while the single disc radius is b_d Thus a collision is computed when the distance between disc center and either rotor end center is less than b_r+b_d

Linear momentum, p, is conserved during a collision.

Let dv=dv₁, then

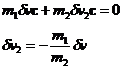
where c is a unit vector pointing from the center of the free disc to the center of the rotor end disc on which the collision is taking place. Let's specialize the masses so that m₁=m_r and m₂=m_d where subscripts r and d correspond to rotor and free disc.

The angular momentum due to rotor's rotation is a combination of the angular momentum due to rotation of the 2 end discs about the axis and that due to rotation of each of the end discs about their own center. The moment of inertia due to the former rotation is ml₀² and the moment of inertia due to the latter rotation is mb_r²/2. For notational brevity we will define the following value for l as a combination of the two quantities in the moment of inertia:

If w is the rotation rate of the rotor, the total initial angular momentum is:

Final angular momentum is:

Setting final equal L to initial L we have

For simple discs, at the moment of collision, r₁-r₂ is parallel to c so the cross product is zero. But, for a disc-rotor collision, the CM of the rotor is not at the center of the end disc so the change in angular momentum is finite.

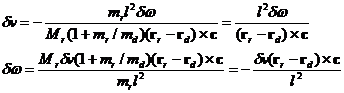
Using the expression for dw in the energy conservation equation below

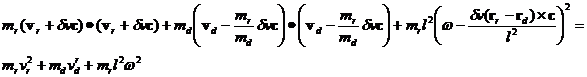we obtain the following expression for dv:

Computation for Two Rotor Collision.

Now let's consider what must be done to modify the above equation when we have two rotors rather than a rotor and a disc. The angular momentum associated with the linear motion of the rotors is the same as before:

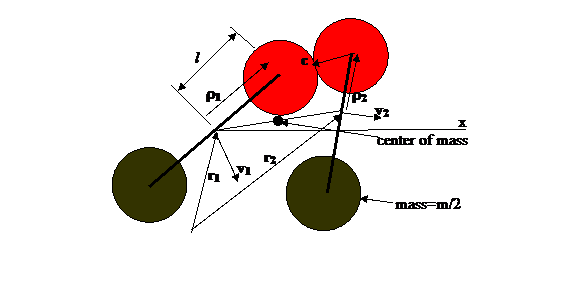
Figure 2: Illustration of 2 rotors colliding . The distance between the centers of the rotor end discs is 2l and the radius of the end discs is b_r Thus a collision is computed when the distance between disc center and either rotor end center is less than 2b_r. r is the vector from the axis of the rotor to the center of its colliding end disc, and c is a unit vector along the line from the center of one rotor's end disc to the center of the one of the end discs of the other rotor.

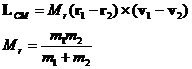
Let dv=dv₁, then

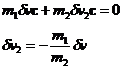
where now the r₁ and r₂ vectors point to the rotation axes of the rotors. However, when we define the conservation of angular momentum there are now two rotation rates, w, to consider.

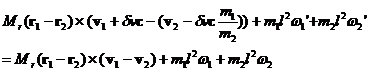
The collision of the rotors results in equal and opposite force impulses, Pc, to the rotor ends in question. We can convert these force impulses to torque impulses via the standard equation for torque:

where r is the vector from the axis of the rotor in question to the center of its colliding end disc. Note that the actual impulse point is at the radius of the end disc and therefore the vector, r_P, to the impulse point is

and the torque impulse becomes

where we have taken into account the fact that c x c=0.

Then the values of the change in w of each of the rotors will be:

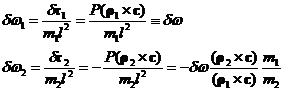
Then the conservation of L equation can be rewritten with just one dw

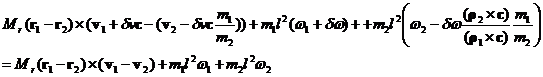
and this equation can be solved in for dw in terms of dv:

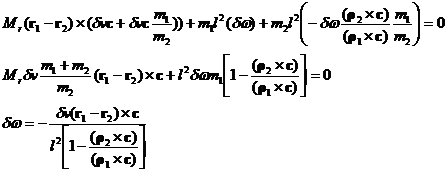
The energy equation is then

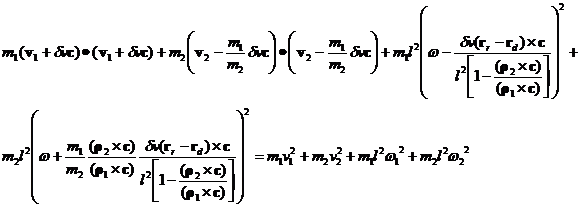
The result for dv is rather messy. To shorten the expression, define f as the following fraction:

Then: