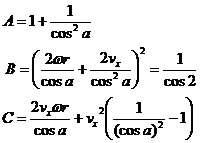Rotor in a Reflective Box
1. Response of a Rotor to an Impulse Applied to One of Its End Masses
The basic driver involved in hard object collisions is an impulse. An impulse is the product of a force times a very small time increment which, of course, leads to a change in momentum like mdv where m is the mass and dv is the change in the velocity. The time increment is small enough that there will be no significant rotation of the rotor or displacement of its center of mass within the duration of the impulse. The significant changes in angle and position will occur after the impulse.
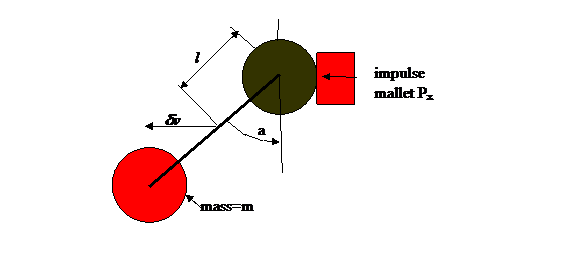
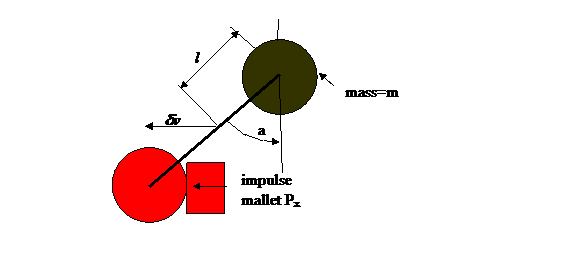
The
specific diagram for this problem is shown below. To make the problem primitive and simple,
both of the initial motions are nil. The final motion will be a combination of
a center of mass velocity, dvx, and a final rotation, at
rate dw, about the center of mass. The impulse is along the -x direction as
shown.
The change in x momentum is a combination of the change in center of mass velocity and rotation speed dw. Here Px is the impulse Fxdt; Note that Px is negative.:
![]()
Solving for dw:
![]()
![]()
The energy supplied by the impulse is Fxdx which
is the same as Px<vx> where <vx>
is the 1/2 of the final speed that will be obtained by the rotor.
Thus conservation of energy requires that:
![]()
Inserting the solution for dw:
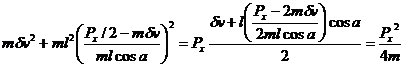
This is a quadratic equation with unknown dv. Computing a, b, and c coefficients of dv2, dv1, and dv0.
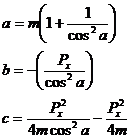
![]()
Solving the quadratic equation for dv we obtain:
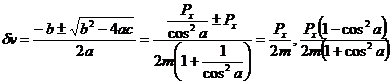
The first solution does not allow for the possibility of spin since it gives dw=0. The second solution is more general and is valid for all cases where cos(a) is not equal to zero.
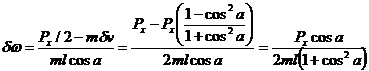
What happens when we apply the impulse to the other end of the rotor?
The change in x momentum is a combination of the change in center of mass velocity and rotation speed dw.
![]()
Solving for dw:
![]()
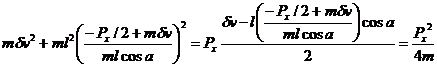
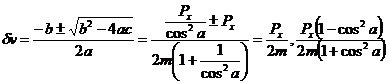
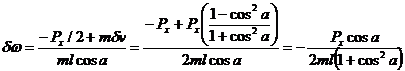
2. Collision with a flat rigid surface
It is expected that the rigid surface collision will result in negation of the normal component of v but the energy of the rotor will not be changed. For this simulation it will also be assumed that there is no friction between the wall and the rotor end. That is, the wall applies no impulse parallel to its surface.
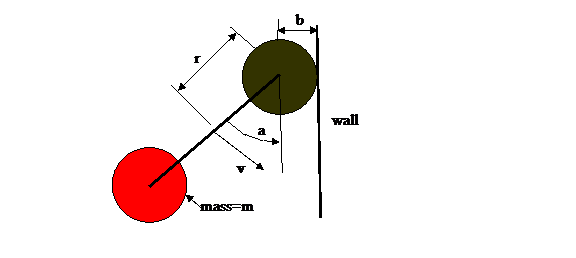
Figure 1: Illustration of rotor hitting surface
x=constant with rotational angle a and center of mass velocity v. The
distance between the centers of the end discs is 2r and the radius of the end
discs is b.
In the case of a collision with a rigid wall, the impulse discussed in section 1 is just twice the negative of the x component of the incident momentum. That means that the normal component of the velocity of the end disc hitting the x=+c wall gets negated. For now, think of w as positive and that the rotation is counter clockwise.
![]()
More generally the equation for the changes of vx and w is:
![]()
where the term on the right hand side is twice the impulse and
![]()
This value of sign for s is valid for both cases, x=+/-c.
Note that the top end can hit the x=+c wall even if its rotational motion in the x direction is opposite its CM motion.
Solving for dw we get:
![]()
The final value of w, w', is the sum of the initial value and dw
![]()
The way that the final motion is divided between rotational and center of mass motion is determined by the conservation of energy. Total final energy is equal to total initial energy. Assuming for now vyCM=0 and dividing out the mass, m, which is common to all terms:
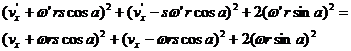
Using trig identities:
![]()
and solving the momentum equation for w' we have:
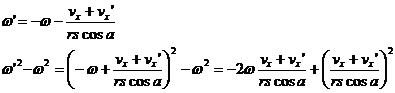
Now we must gather the terms linear in vx' with
coefficient B and squared in vx' with coefficient A and the terms
that don't depend on vx' with value C. Note that s2=1 so we drop it for
notation brevity.
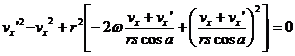
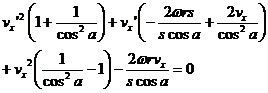
Obviously
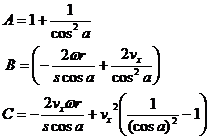
The solutions for vx' are the standard solution
for a quadratic equation:
![]()
For notation simplicity, renaming the quantity 1+b2/(2r2)=d
we have:
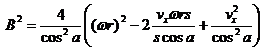
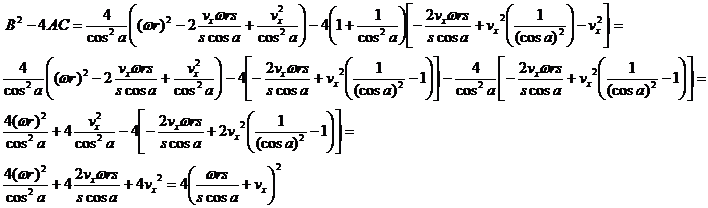
Thus:
![]()
Therefore
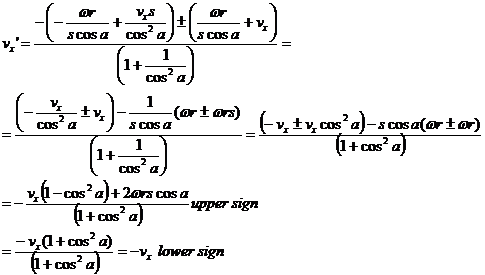
The lower sign gives a solution that conserves energy but doesn't result in mixing of vx' with w so we choose the upper sign solution. However, the upper sign gives positive vx' at the +x wall even when cos(a)>0, w>0, and vx=0. For that reason we have to insert the sign of the initial rotation into this solution.
With that solution we can now state the value of w':
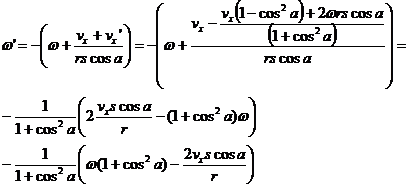
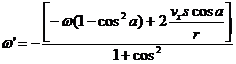
![]()
Let's show that energy is conserved by this solution at least when vy=0:
![]()
We see that the cross product terms in the two components of the expression cancel and the remainder of the terms sum up to
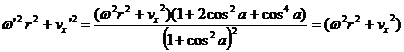
which proves conservation of energy.
By analogy we can clearly state the solution for when the rotor hits a y=constant wall by changing the cosine terms to sine terms. In this case we let s=1 when the black end hits the y=constant wall and let s=-1 when the red hand end hits the y=constant wall.
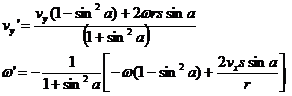
Appendix: Show that CM motion Energy is Orthogonal to Rotational Motion Energy
![]()
Noting that the cross terms in the squares cancel and using some trig identities:
![]()
where ICM=2mr2 is the moment of
inertia of the rotor about its center of mass and m is the mass at either end
of the rotor.