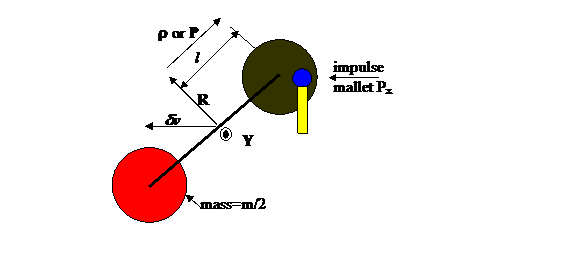Rotor in a Reflective 3D Box
Introduction
The goal of
this animation is to provide a rotational analog to the usual hard sphere
collision problem. The simplest extended
rotating model is that of the symmetric rigid rotor with massive spheres at
each end of a thin rigid rod. Just as in
the hard sphere collision problem, we will make the assumption that the forces
of the collisions are always directed at the centers of the end spheres. This is equivalent to saying that, during the
collision, there is no tangential friction at the surface of the end sphere. As a result of this assumption, spin about
the axis of the rod cannot be induced by collisions since there is no torque
moment about this axis. That is a great
simplification, since then we do not have to solve the Euler equations that
usually couple the spins about the three axes of the rotor even under
torque-free conditions.
1. Response of a Rotor to an Impulse Applied to One of Its Ends
Before we
start, I should say that the bold
character symbols in both text and equations denote vectors or matrices. This avoids the need for putting arrows over
the vectors and matrices.
The basic
driver involved in hard object collisions is an impulse. An impulse is the product of a force times a
very small time increment which, of course, leads to a change in momentum like
mδv
where m is the mass and δv is the change in the velocity. The time increment is small enough that there
will be no significant rotation of the rotor or displacement of its center of
mass within the duration of the impulse.
The significant changes in angle and position will occur after the impulse as results of changes
in angular spin rate or linear velocity.
The
specific diagram for this problem is shown below. To make the problem primitive and simple,
initial center of mass speed and rotation rate are zero. The final motion will
be a combination of a center of mass velocity, δvx,
and a final rotation, at rate δω,
about the center of mass. To start, the
impulse is along the -x direction as shown.
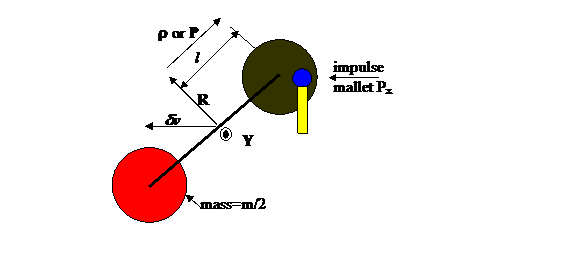
Figure 0: Showing the rotor being hit by a mallet at
an oblique angle with impulse Px. The impulse will cause a combination of rotation about
the Roll (R) and Yaw (Y) axes. The rotation about the pitch (P) axis will
not be affected because there is no torque moment about that axis.
The change in x momentum is a combination of the change in
center of mass velocity and rotation speed δωz. Here Px
is the impulse Fxdt where
Fx is the force in the -x direction; Note that Px is
negative.:
We have to take into account that there are 2 body axes about
which the force impulse can have an effect.
We will arbitrarily call these the roll axis and the yaw axis while the
pitch axis will be along the length of the rod connecting the two end
spheres. Initially the pitch axis will
be the x axis while the roll axis will be along the y direction and the yaw will
be along the z direction (out of and into of the screen). The program will track the orientations of
these three axes and resolve the applied torque into its roll and yaw
components.
The coordinates perpendicular
to ρ can be resolved into parts, one of which is
along the roll axis and one along the yaw axis.
The pitch axis is not important since it can't receive any torque.
|
|
|
(1.1)
|
While the body axes can be important when we have
body-induced forces like on-board thrusters, for the cases analyzed here, all
of the forces will come from external sources like impulses or by being hit by
other bodies so we will just compute the torques and reaction changes in
rotation rates and vectors in the laboratory (x,y,z) coordinate system.
Let's take the case where the impulse is along an arbitrary
unit vector, c, not aligned with any
of the xyz axes. Then we have the following equations:
|
|
|
(1.2)
|
where δv
is the velocity of the center of mass and ρ is the vector from the center of the rotor to
one of its end spheres.
The first of these equations just says that the change in
the component of velocity along the c direction is equal, by Newton's
law, to P/m, where m is the total mass of the rotor. The second and third equation say that the
change in the vector rotation rate, δω, is perpendicular to both c and ρ.
We can re-write equation (1.2)
in terms of its xyz components:
|
|
|
(1.3)
|
Then the matrix and vector expression becomes:
|
|
|
(1.4)
|
|
|
|
(1.5)
|
Solving equation (1.5)
we obtain:
(1.6)
We need to insert the values of δω2
into an energy conservation equation.
|
|
|
(1.7)
|
and then solve the resulting quadratic equation for δvc. Note that:
|
|
|
(1.8)
|
(1.9)
The solutions for δv and δω are then:
|
|
|
(1.10)
|
|
|
|
(1.11)
|
|
|
|
(1.12)
|
The new spin rate vector is ω+δω.
To incrementally change the orientation of the rotor about
this new spin axis, we apply the Rodrigues matrix below:
|
|
|
(1.13)
|
where
|
|
|
(1.14)
|
and δt is the time increment.
2. Collision with a flat rigid surface
It is expected that the rigid surface collision will result
in negation of the normal component of v,
the total velocity due to both rotation and linear motion, but the energy of the rotor will not
be changed. For this simulation it will
be assumed that there is no friction between the wall and the rotor end.
That is, the wall applies no impulse parallel to its surface.
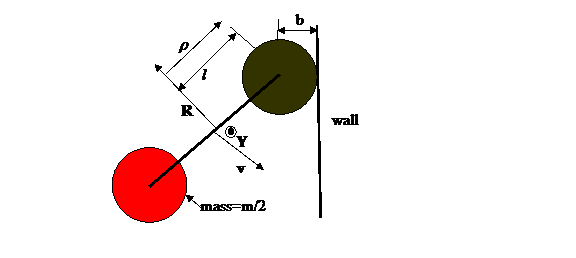
Figure 1: Illustration of rotor hitting surface
x=constant with rotational angle a and center of mass velocity v. The
distance between the centers of the end Spheres is 2l and the radius of the end
Spheres is b. The Roll (R) and Yaw (Y) axes are
shown
In the case of a collision with a rigid wall, the impulse
discussed in section 1 is just twice the negative of the x component of the
incident momentum. That means that the normal
component of the velocity of the end sphere hitting the x=+constant wall gets
negated. For generality, let x=c where c is the unit vector along the outward normal to any of the 6
walls.
(2.1)
where - is equal to the c component of the velocity due to the rotational motion of the
rotor.
Also note that, by definition, ρ and
ω are always perpendicular,
|
|
|
(2.2)
|
Further, the component of ω parallel to c does not result in a change of ω.
|
|
|
(2.3)
|
All of these equations are valid regardless of the
coordinate system in which c, ω and ρ are described.
We simply choose to work in the xyz system and to convert, if needed, to
body rotations afterward. Rewriting
equations (2.1),
(2.2)
and (2.3)
in matrix form and setting c=x for
the general case we have:
|
|
|
(2.4)
|
After taking the inverse of the matrix on the left, the
solution for δω in equation (2.4)
is:
|
|
|
(2.5)
|
The magnitude of the rotational rate after the collision is
given by:
|
|
|
(2.6)
|
where
|
|
|
(2.7)
|
and the new rotation axis unit vector is:
|
|
|
(2.8)
|
which will be the unit vector used in the Rodrigues matrix
of the previous section.
We have one more expression from which to obtain the value
of vc'. The conservation of energy equation is:
|
|
|
(2.9)
|
where ωR' and ωY'
are linear functions of v'c.
Once we've inserted their v'c
dependence into equation (2.9), we can solve what will
be a quadratic equation for v'c.
The result is
|
|
|
(2.10)
|
Then the new value of the CM speed is
|
|
|
(2.11)
|
The value of δω after inserting the new value v'CM into
equation (2.5)
is:
|
|
|
(2.12)
|
(2.13)
Rotor-Sphere Collisions
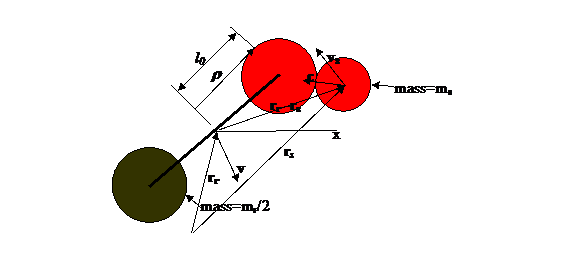
Figure 2: Illustration of rotor and a free
sphere. The rotor rotational angle is a and center of mass velocity v The distance
between the centers of the rotor end spheres is 2l0 and the radius
of the end Spheres is br while the single Sphere radius is bs
Thus a collision is computed when the distance between Sphere center and either
rotor end center is less than br+bs
For the
case of a Rotor and a free Sphere, the linear momentum associated with the Sphere
and rotor center of mass (CM) velocity must be conserved and the angular momentum,
LCM, associated with their linear momentum about their CM as well as
the simple rotational angular momentum, Lω,
of the Rotor must be conserved. Having
used the linear and angular momentum conservation equations to compute the new
values of Rotor rotation rate, we must then use the conservation of energy
equation to compute the new values of their relative velocity with respect to
their previous velocities. These results
will always center around their c unit vector which is the vector between the
center of the Sphere and the center of the rotor end with which it collides. Recall from the previous 2D Rotor
calculations that the angular momentum associated with the linear motion of the
2 masses is:
|
|
|
(2.14)
|
where the subscripts r and s refer to the values for the
rotor and free sphere and the ms are their masses, respectively.
The angular momentum of the rotor about its axis is:
|
|
|
(2.15)
|
and the linear momentum of the 2 masses is:
|
|
|
(2.16)
|
The velocities of the two masses will change along
the c vector. If we name the as yet unknown magnitude of
the rotor CM speed change δv,
then, from equation (2.16),
the Sphere speed change will be -(mr/ms)δv.
The expression for the conservation of angular momentum of is a bit more
elaborate. The equation for the final
angular momentum is:
|
|
|
(2.17)
|
while the initial angular momentum is:
|
|
|
(2.18)
|
To compute the final rotor rotational angular momentum, we
need to set equations (2.17) and (2.18)
equal to each other:
|
|
|
(2.19)
|
Solving equation (2.19)
for the change in ω we obtain:
|
|
|
(2.20)
|
|
|
|
(2.21)
|
With some vector algebra we can rewrite the right hand side
of equation (2.21)
in terms of ρ,
the vector that points from the rotor axis to the center of its end sphere:
|
|
|
(2.22)
|
which guarantees that the condition for constancy of spin
angular momentum will exist:
|
|
|
(2.23)
|
The conservation of energy equation dictates that the
following equation must be true:
(2.24)
|
|
|
(2.25)
|
(2.26)
The result for δv is:
|
|
|
(2.27)
|
Then δω becomes
|
|
|
(2.28)
|
Rotor-Rotor Collisions
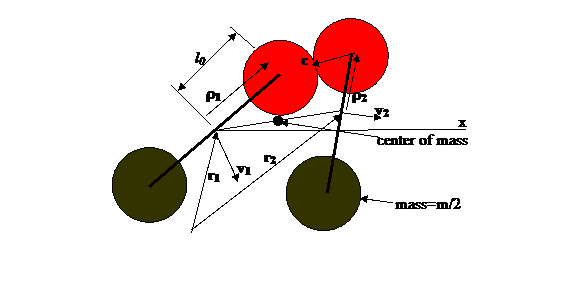
Figure 3: Illustration of 2 rotors colliding . The distance between the centers of the
rotor end Spheres is 2l and the radius of the end Sphere is br Thus a collision is computed when the
distance between Sphere center and either rotor end center is less than 2br. ρ is the vector
from the axis of the rotor to the center of its colliding end Sphere, and c is a unit
vector along the line from the center of rotor 2s end Sphere to the center of
the end spheres of rotor 1.
For
collisions of two Rotors, the linear momentum associated with their center of
mass (CM) velocity must be conserved and the angular momentum, LCM,
associated with their linear momentum about their CM and their simple
rotational angular momentum, Lω,
of the Rotors must be conserved. Having
used the linear and angular momentum conservation equations to compute the new
values of Rotors' rotation rates, we must then use the conservation of energy
equation to compute the new values of their relative velocity with respect to
their previous velocities. These results
will always center around their c
unit vector which is the vector between the center of one rotor end sphere and
the center of the other rotor end with which it collides. Recall from the previous 2D Rotor
calculations that the angular momentum associated with the linear motion of the 2 Rotor masses is:
|
|
|
(3.1)
|
The final angular momentum after the collision can be
written:
|
|
|
(3.2)
|
and the initial angular momentum before the collision can be
written
|
|
|
(3.3)
|
We may set equations (3.2)
and (3.3)
equal getting the following equation:
|
|
|
(3.4)
|
First let's rewrite in terms of ρ1 and ρ2. Note that the vector expression relating is
|
|
|
(3.5)
|
Then solving for we have
|
|
|
(3.6)
|
so we can rewrite equation (3.4)
|
|
|
(3.7)
|
Since the same (unknown)
impulse, P, causes both ω1
and ω2
to change, there is a specific relationship between their changes.
Let both torque impulses be described in terms of the
unknown value of P
|
|
|
(3.8)
|
Dot multiply both sides of the equation for by and we have:
|
|
|
(3.9)
|
Then the solution for P is gotten by solving equation (3.9)
|
|
|
(3.10)
|
And then we can use our result for P in the δω2 equation:
|
|
|
(3.11)
|
We may rewrite equation (3.11) as
a matrix multiplied by δω. First, for brevity, rename some of the
quantities in equation (3.11):
|
|
|
(3.12)
|
Now writing out the components of v2 and we find the following matrix:
|
|
|
(3.13)
|
where M21
is the dyadic tensor a2a1.
Then equation (3.7)
can be solved as:
|
|
|
(3.14)
|
so that the solution for δω is:
|
|
|
(3.15)
|
where the bold 1
in equation (3.15)
denotes the unit matrix.
Now we can write the conservation of energy equation for the
two rotors
|
|
|
(3.16)
|
Simplify notation for equation (3.15)
|
|
|
(3.17)
|
where
|
|
|
(3.18)
|
where a is a
vector. Then solving equation (3.16)
we obtain:
|
|
|
(3.19)
|
Recalling equation (3.15)
for δω we have:
|
|
|
(3.20)
|
4. Relation Between Rotor Angular Orientation and its Spin Axis Vector, ω,
in Torque Free Rotation
Having
obtained the value of ω consistent with the value of ρ, we
need to decide how to rotate the rotor.
The rotor spins about the ω vector at the rate ω. In order to display this spin motion we need
to use a matrix that rotates points about an axis parallel to ω in space.
The Rodrigues formula http://en.wikipedia.org/wiki/Rodrigues%27_rotation_formula
is such a matrix and for our case of ρ and ω is written:
|
|
|
(4.1)
|
where ω with the carat on top denotes a unit vector in
the ω direction and ρ' is the new vector from the axis to
the Rotor end sphere and is the rotation angle (usually small) about
the axis.