Sagnac Effect
Introduction
The Sagnac effect is important in technology because the time differences for photons to propagate around a rotating disk is, to first order, linearly proportional to the angular speed of the disk. That effect permitted the development of the ring laser gyro and the fiber-optic gyro which are both very low maintenance and high accuracy gyros.
Discussion
Figure 1 is a diagram of the Sagnac
effect animation. Please read the caption.
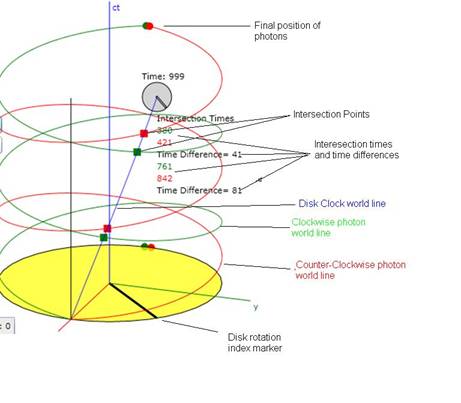
Figure 1: Diagram of the Sagnac Effect animation. The clockwise (looking along the negative ct direction) photon as well as its helical world line is green and the counterclockwise photon is red. Note that the square intersection points are color-coded to match the intersecting photon color. Also note that the time difference for the second pair of intersections is twice that of the first pair.
Calculations
The time required for a photon to circumnavigate the rim of he disk integer n times is
![]() (1)
(1)
where R is the radius of the disk and c is the speed of light. The equation for the time of intersection is then:
![]() (2)
(2)
where the - sign corresponds to
photons propagating in the same direction as the disk rotation and vice-versa.
Solving this equation and using equation 1 we have:
![]() (3)
(3)
where b=v/c.
For technology, it is important to know the time difference between the nth CW intersection and the nth CCW intersection:
![]() (4)
(4)
We see from equation 4 that the result is, for small b, linear in b and reverses sign when b reverses sign.
Let’s insert some numbers into equation 4.
Assume the following:
R=1 meter
W=1 radian per second
Then
![]()
so that
![]()
Because the frequency of a typical laser gyro is approximately f0= 5x1014 Hz, this time difference corresponds to a phase difference between CW and CCW waves of
![]()
Since this laser gyro has a free spectral range of
![]()
the phase difference cited here corresponds to a frequency splitting of:
![]()
The overall equation for the frequency splitting of a circular laser gyro of radius R turns out to be
![]()
where l is the wavelength of the laser.