Charge Flow in a Single Resistor

Introduction

This animation shows the behavior of charge carriers that contribute to the current in a resistor. It takes into account their collisions with the background lattice of the medium which provides the impedance to charge flow. It assumes both the carriers and the background lattice (scatterers) have thermal motion, the former being random translation throughout the resistor and the latter being simple harmonic motion about the nominal position of the nucleus in the lattice.

Figures

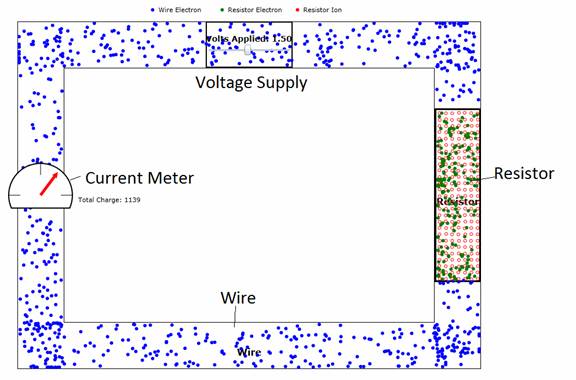
Figure 1: Snapshot of the animation labeling scatterers, electrons, and current meter. The rate of electron flow in the wire is driven by the rate of charge arrival at the top of resistor.

Voltage Drop

The current must equal the Voltage drop, V, divided by the resistance, R. The current is also defined as the product of the carrier particle charge, e, times the carrier density n and the drift speed, v_d, times the cross-sectional area of the resistor, A.

The drift speed is the only quantity that requires more physics explanation. The equation for drift speed is

where E is the electric field, E=V/L, V is the applied voltage, L is the length of the resistor, m is the carrier mass, script l is the mean free path between carrier scatterings and v_thermal is average the thermal speed of the carriers. An equation for script l is the following:

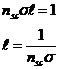
where n_sc is the density of carrier scatterers (often much greater than the density of carriers themselves) and s is the combined scatterer-carrier scattering cross section which has units of length squared. It's important to note that the probability of electrons scattering from other electrons is much lower than the probability of electrons scattering from the background lattice. We see that v_d, and therefore I, is inversely proportional to n_sc.

where N_sc is the total number of scatterers in the resistor.

Therefore we can write the current as:

where N_c is the total number of electrons in the resistor. It can be seen from this equation that the resistance, R, is

Sliders are provided for the user to adjust both N_sc and N_c.

Thermal Noise Current

Due to the random thermal motion of the charge carriers, some noise current is generated even when there is no applied voltage. This current is computed from the number of carriers hitting the top and bottom of the resistor per time increment. The root mean square of the noise current is expected to be:

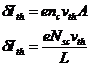
where N is the total number of carriers in the resistor and L is its length. If v_th=1 length increment per time increment and numerically N=L=300, then we expect the thermal noise to be one charge per time increment. This is approximately realized in the program.

The mean value of the thermal speed can be expressed in terms of temperature:

How the Program Works

The initial positions of the charge carriers are chosen randomly inside the resistor's rectangular outline. The initial positions of the lattice nuclei are chosen to be in a square lattice inside the resistor's rectangular outline. The initial phases of the motion of the lattice nuclei are also chosen randomly. The amplitudes of the nuclei simple harmonic motion are set to be uniform but the directions of this motion are chosen to be random. The initial thermal velocities of the carriers are set to be between 0 and a user-chosen maximum.

The carrier is accelerated by the electric field provided by the source voltage. The acceleration continues unabated until the carrier collides with a scattering nucleus. During the acceleration it is important to make the product of the program's time increment, dt, and thermal speed considerably less than the expected distance between scatterings.

Otherwise the electrons would just blow right past the scatterers without being impeded by them.

It is also important to keep that same product much less than the length L of the resistor which is usually a less restrictive condition than the previous one since A/(Ns) is generally much less than 1.

At the point of scatter the carrier has reached some reasonable fraction of its drift velocity (as discussed in the previous section) but most of this speed is lost (in fact it is negated part of the time) when the carrier is backscattered by the nucleus. For simplicity, the program assumes that the drift speed becomes zero at this point. Then the acceleration process is repeated. As a result of the drift speed, the carrier makes progress toward the output end of the resistor.

Summary

The animation is a reasonably valid simulation of charge flow in conductors where the carriers have both thermal motion and a voltage-induced drift velocity. The thermal motion of carriers gives rise to thermal noise (often called Johnson noise) that is seen as the fluctuations of the current meter. The learner may study both the average current and the thermal noise as a function of thermal speed, voltages, carrier density, scatterer density, and carrier-scatterer collision cross section.