Physics of a Siphon

Introduction

            One of the more interesting experiments that a learner can do is to observe the action of a siphon.  All he/she needs is a pail of water and a flexible tube which, ideally, would be transparent so that the flow can be seen.  Another ideal condition would be to have some small particles in the water that have about the same density as water but a different index of refraction so that the steady state flow rate throughout the tube can be seen. 

            The learner would initially fill the tube with water by submerging it in the pail and then remove one end while holding the thumb over it (or inserting a rubber stopper) and then lower that end below the level of the water in the pail.  After removing the thumb or stopper, water starts to flow up over the rim of the pail and out of the end of the tube.  The flow would continue until the water level in the pail becomes lower than the height of the inlet end of the tube and the remaining water in the tube is exhausted.

Figures:

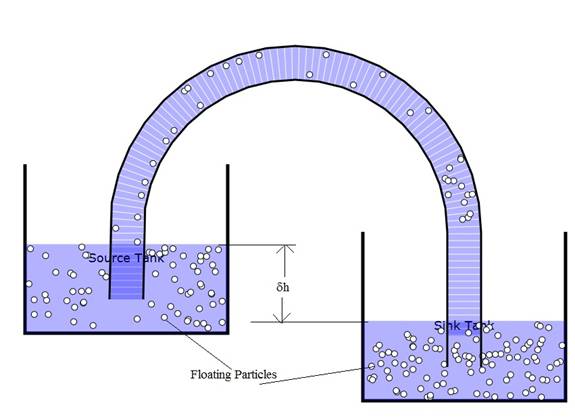
Figure 1: Illustration of a siphon.  The symbol δh shows the difference between the source and sink surface levels which determines the rate of flow in the siphon pipe.

Rate of flow

            When a fluid particle of mass m falls the height δh in gravity it gains kinetic energy δΕ equal to mgδh

δE= 1 2 m v 2 =mgδh MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiabes7aKjaadw eacqGH9aqpdaWcaaqaaiaaigdaaeaacaaIYaaaaiaad2gacaWG2bWa aWbaaSqabeaacaaIYaaaaOGaeyypa0JaamyBaiaadEgacqaH0oazca WGObaaaa@433D@  

(1.1)

where g is the acceleration of gravity.

The particle therefore speeds up to a velocity v where

v= 2gδh MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadAhacqGH9a qpdaGcaaqaaiaaikdacaWGNbGaeqiTdqMaamiAaaWcbeaaaaa@3C41@  

(1.2)

Equation 1.2 is a good estimate of the flow rate of the liquid in Figure 1.  It does not take into account the drag due to the viscosity of the liquid or the due to the roughness of the inner walls of the pipe.

Maximum Height Above Liquid Surfaces

            The maximum elevation over which the siphon can flow is dictated by the ambient pressure, P0, in combination with the cohesiveness, like surface tension, of the liquid.  For most liquids at earth's surface, ambient pressure is by far the dominant component.  At the liquid surfaces, we have pressure P0 which results in a compressive-like stress on the two columns of water.  If we could measure the pressure as a function of height above the surfaces, we would find that this compressive stress is reduced by the following equation

P(h)= P 0  −ρgh MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadcfacaGGOa GaamiAaiaacMcacqGH9aqpcaWGqbWaaSbaaSqaaiaaicdacaaMc8oa beaakiabgkHiTiabeg8aYjaadEgacaWGObaaaa@41E2@  

(1.3)

where ρ is the density of the liquid.  At height

h Max = P 0 ρg MathType@MTEF@5@5@+= feaagKart1ev2aaatCvAUfeBSjuyZL2yd9gzLbvyNv2CaerbuLwBLn hiov2DGi1BTfMBaeXatLxBI9gBaerbd9wDYLwzYbItLDharqqtubsr 4rNCHbGeaGqiVCI8FfYJH8YrFfeuY=Hhbbf9v8qqaqFr0xc9pk0xbb a9q8WqFfeaY=biLkVcLq=JHqpepeea0=as0Fb9pgeaYRXxe9vr0=vr 0=vqpWqaaeaabiGaciaacaqabeaadaqaaqaaaOqaaiaadIgadaWgaa WcbaGaamytaiaadggacaWG4baabeaakiabg2da9maalaaabaGaamiu amaaBaaaleaacaaIWaaabeaaaOqaaiabeg8aYjaadEgaaaaaaa@3F4A@  

(1.4)

P(h)=0 and there is no compressive stress to hold the two columns of water together so both start to fall back into their respective containers leaving a gap at the top of the siphon which breaks the siphon circuit.