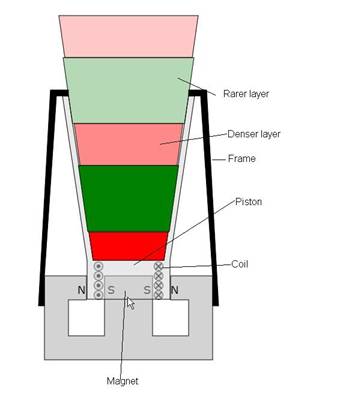
Speaker Piston Motion and Resulting Density Layers
Figure 1: Diagram
showing the coil, magnet, piston and frame.
Also shown are several density layers.
Red corresponds to a positive density increment and green corresponds to
a negative density increment.
Force on the current-carrying coil
Figure 1 shows the coil immersed in an axi-symmetric magnetic field, B, which points inward (from North to South) toward the center of the coil. The equation for the force on a short section, dl, of the coil wire with current, i, is
![]() (A)
(A)
where i
is the current in amperes, dl is the length in meters and this equation results
in a force increment, dF, in
![]()
where rcoil
is the radius of the coil and neff is the effective number of
coil turns immersed in the field. As can
be seen from the diagram, when the current is flowing away from us on the right
hand side of the coil, the sign of the result in equation A is positive and the
coil moves upward. In this animation it
is assumed that the coil’s current frequency is much less than any resonance
the speaker coil mass and diaphragm might have so there is no phase lag between
current reversals and coil direction reversals.
Density Layer Thickness and Position Calculations
Let the motion of the plane of the speaker be described by:
![]() (1)
(1)
so that speaker’s y starts at 0 and
when wt=p
is upward by distance 2A. Assume the wave is going upward at speed vs
Then the thickness of the wave when w*t<p is:
![]() (2)
(2)
so that the final thickness is
![]() (3)
(3)
When the speaker plane starts downward at wt=p from a position y=2A the present layer is launched at the speed of sound and a new density layer is formed and its thickness varies as:
![]() (4)
(4)
so that its final thickness is:
![]() (5)
(5)
Thus the thickness difference is 4A.
We can now ask the question “Where is the bottom of the first layer with respect to the top of the second when the second is ejected”? First note that, upon ejection, the bottom of the second layer is at y=0 since 1-cos(wt)=0. The top of that layer is at y=Tf2. The bottom of the first layer started at y=2A when at wt=p and is now at position
![]() (6)
(6)
Therefore the bottom of the first layer is at the same position as the top of the second layer and since both now travel upward at rate vs this condition will remain fixed.
Subsequent layer doublets will repeat the first doublet’s
behavior.
Radius matching calculations
The radius of the bottom of any layer at launch is always rp, the radius of the piston The radius at the top of the layer at launch depends on the angle of the cone. For the case of the second (thicker) layer, where the piston is at y=2A, the vertical distance from the piston to the top of the frame is h0-2A where h0 is the height of the cone. Then the radius at the top of this layer is
![]() (7)
(7)
where rc is the radius of the top of the cone.
By the same reasoning, the radius at the top of the thinner layer where the piston is at y=0 is
![]() (8)
(8)
Here is the dilemma: if the shape of the first layer at launch remains the same until the second layer is ready to launch, does the radius of the bottom of the first layer equal the radius of the top of the second layer at that time? To answer that question, recall that the radius of the first layer expands by the factor (rc-r0)/h0*dy where dy is the velocity of sound motion that the bottom undergoes.
![]() (9)
(9)
Now I will substitute the value for Tf2 into equation 7 so we can compare these 2 results
![]() (10)
(10)
The difference is:
![]()
which results in

The difference is small if A/h0 is small or the difference rc-rp is small. The conclusion of this section is that we should expect some mismatch in the radii of the two layer types.
Expansion and Diffusion Effects
As can be seen in Figure 1, the red and green of the density
layers tends to fade as the layers progress away from the speaker piston. This would be due to the horizontal widening
of the layers as well as the molecular diffusion out of regions of higher or
lower density. I have made no attempt to
accurately compute these effects but the viewer should be aware that they exist.