Design and Animation of a Spectroscope
Introduction
The prism spectroscope provided the experimental foundations of early astronomy and early atomic physics. It is important to understand the design and operation of this fundamental device of optics.
Design
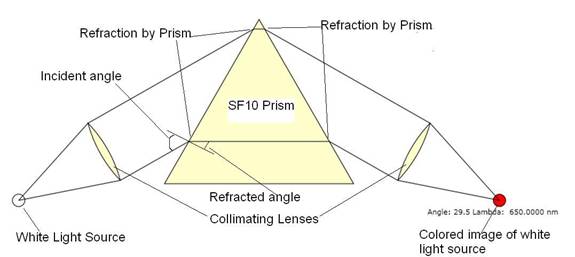
Figure 1: Design of a prism spectroscope. As shown in
the figure, the angles of the source arms and image arms are symmetrical with
respect to the axis of the prism. This
symmetry results in what is called the angle of minimum deviation where, if the
prism were to be rotated about its z axis, the vertical position of the image would
go through a minimum.
The prism is the most critical component of the spectroscope. In order to easily resolve small differences in wavelength of the input source, it must have a large variation of index of refraction with wavelength. The prism used in this animation is Schott SF-10[1] which is a dense flint glass. It provides a value of dn/dl =-0.129 mm-1 at the sodium D line wavelength of 0.5876 mm.
Calculations
The most important calculation is the angle of incidence on the prism for a given index of refraction, n, needed to obtain the symmetry shown in Figure 1. Let the half-angle of the vertex of the prism be called qp. Then it is obvious that the refraction angle with respect to the normal on the left side of the prism is also qp. We may use Snell’s law of refraction to compute the incident angle, qi with respect to the normal of the left side of the prism:
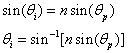(1)
The other important calculation is the wavelength that corresponds to the angle of incidence in Equation 1. The index of refraction of SF-10 Vs. wavelength is given by the following Sellmeier equation.
In order to make the calculation of l Vs qi we perform the following half-step root
finding routine. First, from equation 1,
we find n in terms of qI and
qp
(2)
Then
we iterate through the following loops to find that a value of index of
refraction that agrees with n found in equation 2 within a tolerance tol:
lam0=0.2,lamMax=1.1,lam=lam0,dlam=0.1,tol=0.0001,dn=1;
sol=false;
while(sol==false)
{
dn=indexSF10(lam)-n;
if(Math.Abs(dn)<tol ) sol=true;
if(lam<lamMax)
{lam+=dlam;
}
else
{lam=lam0;dlam=dlam/2;}
}
return lam;