Drude-Lorentz Theory of Dielectric Constant and speed of light in solids
The equation of motion for an electron that is bound by a simple
spring of spring constant k is
![]() (1)
(1)
where m is the mass, b is the drag
coefficient, and e is the electron charge.
This equation is most easily solved by converting to a complex
number format where E(t) and x(t) are the real parts
of
![]()
Then equation 1 becomes:
![]()
or solving for x0:
![]() (2)
(2)
Equation 2 is usually written in the form:
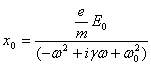 (3)
(3)
where ![]() .
.
The real part of the equation 3 is:
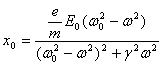 (4)
(4)
In a relatively transparent medium, ![]() . Also for the purposes
of this document, we will assume that
. Also for the purposes
of this document, we will assume that ![]() which means that the
electric field frequency is not near any absorption resonances of the nearly
transparent medium. Then equation 4
becomes:
which means that the
electric field frequency is not near any absorption resonances of the nearly
transparent medium. Then equation 4
becomes:
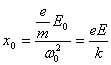
which is the expression for x0
in a static electric field. This just means that the electron experiences
no delay in following the electric field.
The
dipole moment associated with a single electron is then
![]() (5)
(5)
If there are n such electrons per unit volume then the polarization, P, per unit volume is:
![]()
In SI units, the expression for the displacement field, D, in terms of E and/or P is:
![]()
But using expression 5 we have:
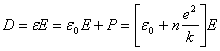 which
also has units if polarization per unit volume and
which
also has units if polarization per unit volume and
which indicates that
![]()
where ![]() . (6)
. (6)
Since k is expressed in
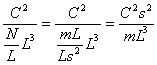 where
C is coulombs, s is seconds, m is kg, and L is meters.
where
C is coulombs, s is seconds, m is kg, and L is meters.
The units of e0
are also ![]() as seen in http://www.ebyte.it/library/educards/sidimensions/SiDimensionsAlfaList.html#f
as seen in http://www.ebyte.it/library/educards/sidimensions/SiDimensionsAlfaList.html#f
Therefore, e1 has the same units as e0.
One might want to know what is the quotient n/w02 to make e1=e0?
![]()
Thus e1 is to be compared with e0 which is the polarizability of free space. The speed of light in the medium is proportional to

where m0 is the magnetic
permeability and is not an important variable in most transparent media.
Therefore higher dipole density and lower resonant frequency tend to reduce the speed of light. Alternatively, if the electron charge were increased and the electron mass decreased, then the speed would also be reduced.
Note that e1m0 has the units: (Where A=Amps, sec=seconds, m=meters kg=kilograms)

where the units of m0 are Newtons A-2.
In comparison to shear waves in solids which have speed:
![]()
where E is the stiffness (Newton/m2) , r is the mass density (kg/m2), and n the Poisson ratio. In the limit that e1>>e0, the equivalent of the stiffness to density ratio is
![]()
On the right hand side, the electron mass density is:
![]() thus:
thus:
![]()
and therefore the shear stiffness G=E/(2(1+n)) corresponds to
![]()
where w02 =k/m
and k is the spring constant (N/m) of the bound electron.
The units of m0
are Newton/Amp2 and therefore the units of the denominator are N-sec2
And the overall units of Gequiv
are ![]()
as expected.
Note from the calculation below that the electromagnetic “stiffness” is ~1015 Nt/m2 compared to the typical 2x1011 N/m2 stiffness of steel. In addition, the electron mass density is small, on the order of 10-2 kg m-3 versus 104 kg m-3 for steel. The ratio of the speed of light in solids to the speed of sound in solids is of the order of 2e8/2e3=1e5 as expected from the above quantities.
Another way to view the effect of e1 on the speed of light in a solid is to assign
fictitious electrons with fictitious density, nv, and fictitious spring constant, kv, to all of vacuum and thereby create a
fraction with the same value as e0
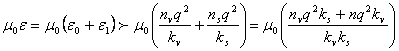
where nv/kv
is of the same order of magnitude as ns/ks.
The consequence of this is that the spring constant assigned
to vacuum acts in series (rather
than in parallel) with the spring constant assigned to the electrons in the
solid thereby reducing the combined stiffness and thereby reducing the speed of
light in the solid. Also note that the
speed is reduced whether e1
exceeds e0 or otherwise.
