Drude-Lorentz Theory of Dielectric Constant and speed of light in solids

The equation of motion for an electron that is bound by a simple spring of spring constant k is

(1)

where m is the mass, b is the drag coefficient, and e is the electron charge.

This equation is most easily solved by converting to a complex number format where E(t) and x(t) are the real parts of

Then equation 1 becomes:

or solving for x₀:

(2)

Equation 2 is usually written in the form:

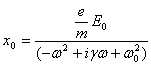(3)

where .

The real part of the equation 3 is:

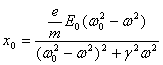(4)

In a relatively transparent medium, . Also for the purposes of this document, we will assume that which means that the electric field frequency is not near any absorption resonances of the nearly transparent medium. Then equation 4 becomes:

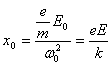
which is the expression for x₀ in a static electric field. This just means that the electron experiences no delay in following the electric field.

The dipole moment associated with a single electron is then

(5)

If there are n such electrons per unit volume then the polarization, P, per unit volume is:

In SI units, the expression for the displacement field, D, in terms of E and/or P is:

But using expression 5 we have:

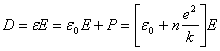which also has units if polarization per unit volume and

which indicates that

where . (6)

The units of

Since k is expressed in Newtons (kg-meter/sec²) per meter, the above expression has units

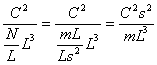where C is coulombs, s is seconds, m is kg, and L is meters.

The units of e₀ are also as seen in http://www.ebyte.it/library/educards/sidimensions/SiDimensionsAlfaList.html#f

Therefore, e₁ has the same units as e₀.

One might want to know what is the quotient n/w₀² to make e₁=e₀?

Thus e₁ is to be compared with e₀ which is the polarizability of free space. The speed of light in the medium is proportional to

where m₀ is the magnetic permeability and is not an important variable in most transparent media.

Therefore higher dipole density and lower resonant frequency tend to reduce the speed of light. Alternatively, if the electron charge were increased and the electron mass decreased, then the speed would also be reduced.

Note that e₁m₀ has the units: (Where A=Amps, sec=seconds, m=meters kg=kilograms)

where the units of m₀ are Newtons A^-2.

In comparison to shear waves in solids which have speed:

where E is the stiffness (Newton/m²) , r is the mass density (kg/m²), and n the Poisson ratio. In the limit that e1>>e0, the equivalent of the stiffness to density ratio is

On the right hand side, the electron mass density is:

thus:

and therefore the shear stiffness G=E/(2(1+n)) corresponds to

where w₀² =k/m and k is the spring constant (N/m) of the bound electron.

The units of m₀ are Newton/Amp² and therefore the units of the denominator are N-sec²

And the overall units of G_equiv are

as expected.

Note from the calculation below that the electromagnetic “stiffness” is ~10¹⁵ Nt/m² compared to the typical 2x10¹¹ N/m² stiffness of steel. In addition, the electron mass density is small, on the order of 10^-2 kg m^-3 versus 10⁴ kg m^-3 for steel. The ratio of the speed of light in solids to the speed of sound in solids is of the order of 2e8/2e3=1e5 as expected from the above quantities.

Another way to view the effect of e₁ on the speed of light in a solid is to assign fictitious electrons with fictitious density, n_v, and fictitious spring constant, k_v, to all of vacuum and thereby create a fraction with the same value as e₀

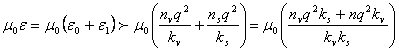
where n_v/k_v is of the same order of magnitude as n_s/k_s.

The consequence of this is that the spring constant assigned to vacuum acts in series (rather than in parallel) with the spring constant assigned to the electrons in the solid thereby reducing the combined stiffness and thereby reducing the speed of light in the solid. Also note that the speed is reduced whether e₁ exceeds e₀ or otherwise.