Collisions of Spheres of Same Mass
Introduction
The following documents the calculation of final trajectories of colliding spheres. For simplicity I will first assume that the second sphere is not moving and, further, both spheres have the same radius and mass. I will compute the trajectories of these spheres as a function of the impact parameter which is defined as the offset between the line along which the center of the incoming sphere approaches and the center of the second sphere as shown in the diagram below.
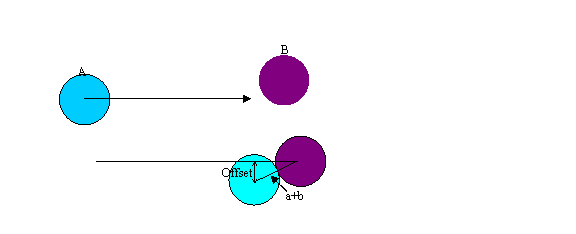
Figure 1: Top shows the incoming sphere from the
left. Bottom shows the configuration at
the moment of impact. The radii of the
spheres are a and b, respectively.
Calculations
There are some important parameters shown in Figure 1. First, note that the momentum transfer, Dp, must be along the line of the radii a+b. This line is at angle
![]() (1)
(1)
where o is the offset between centers shown in Figure 1. Also note that the momentum transferred to A is the negative of the momentum transferred to B:
![]() (2)
(2)
The other requirements for this (assuming an elastic collision) are that the final total energies and momenta must be the same as the initial values (in this case, that of sphere A).
![]() (3)
(3)
When the masses are equal, as assumed here initially, equations 3 yield a useful relationship between the directions of pA and pB. If we write out the expressions for energy and momenta in terms of the velocities, v, we have:
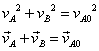 (4)
(4)
where m has been omitted on both sides of the equations. We can take the dot product of both sides of the velocity vector equation and obtain:
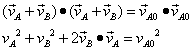 (5)
(5)
Comparing the second line of equation 5 with the first line of equation 4 we must conclude that
![]() (6)
(6)
which means that vector vB must be perpendicular to vector
Also, because the only momentum that sphere B gets is along
the line of centers (at angle a) we
also then know that pA is at angle a-p/2 with respect to the x axis.
Now let’s combine the geometry information we have just derived with the conservation equations to get the velocity vectors after the impact. We can separate the momentum equation into x and y components as follows:
![]() (7)
(7)
From the second equation we get the ratio vB/vA. And then we solve the first equation for both vA and vB in terms of vA0.
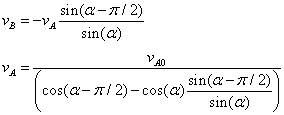 (8)
(8)
![]()