Multilayer Dielectric Fields Documentation
John Rahn
Introduction
This web page gives a really comprehensive view of the performance of any bi-periodic layered structure upon which waves are incident. These waves can be electromagnetic (light and lower frequency as well), acoustic (elastic), or the quantum waves which result from the Schrodinger wave equation. The user inputs to the stack are the optical index of refraction of the structure. To see how the results apply to acoustic and quantum waves, see the Appendix.
I chose to make the period of the multilayer stack exactly ˝ wave at the nominal wave vector, kV0.
kV0=2p/lV0
where lV0 is the design wavelength in vacuum. Since I plot the power reflection coefficient versus kV=2p/lV and the kV for the field calculation can be selected (kVRatio) at will, this choice of periodicity of the design is completely general. To further increase the generality of the result, the ratio of the phase thickness of the low index component to that of the high index component (LHRatio) can also be selected.
In order to convert the structure to a very narrow band transmission filter, I also included a checkbox to place a half wave low index layer in the center of the stack.
The light in this calculation is incident from the left.
When computing the field distribution, one uses a slider to select the ratio of kV to kV0. The field squared, E2, is presented superposed on a plot of the index of refraction. For a good reflector, most of E2 is concentrated at the left of the layered structure.
Multilayer stack wave picture information
This animation shows the effects of varying the wavelength of the incident entity be it electromagnetic radiation, acoustic waves, or quantum de Broglie waves associated with reflections in crystalline solids.
The simple one dimensional stack used in the animation is as shown below:
Substrate
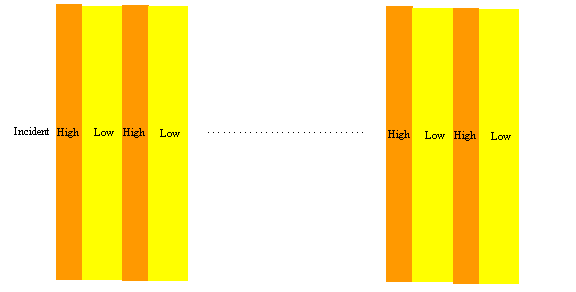
Figure 1: Layout of a multilayer stack. The waves enter the stack from the Incident
medium and exit into the Substrate medium.
The thickness of the orange High layer and the yellow Low layer are such
that their total phase
thickness at the design wavelength and angle are ˝ wave.
At each interface in the above picture, the physical requirement is that the tangential components of the fields be the same (i.e. continuous) on both sides of the interface even though the angles of propagation are different. Those fields include both the left-propagating (reflected) and right-propagating (transmitted) fields. For electromagnetic waves, both the electric fields, E, and the magnetic fields, H, are included in this requirement. For a very thorough explanation of how the electromagnetic fields, reflection coefficients, and transmission coefficients are computed see the Reference[1].
Below is shown, with a complete description in the caption, a typical output for the animation.
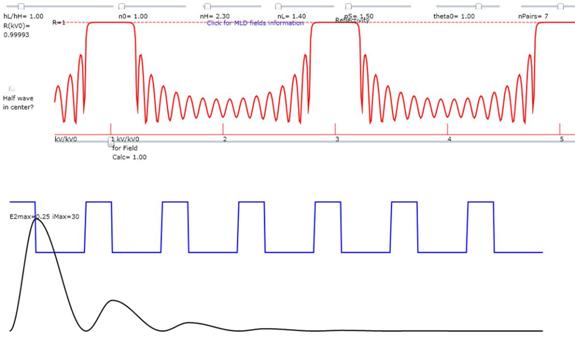
Figure 2:Results of the
calculation of the fields Vs position in the stack. The relative index of refraction Vs position
is given by the blue trace. The square of the field intensity is given by the
black trace. The red trace shows the
reflected power ratio to the incident power Vs the vacuum wave number ratio kv/kv0,
Just below the red trace is a slider which adjusts the ratio kv/kv0
where kv is 2p/l and kv0 is 2p/l0 with l0 being the design wavelength for which the stack pairs
optical thickness is exactly ˝ wave. The sliders above the red trace, from left
to right, adjust
the following:
1. The ratio of Low layer thickness to High layer
thickness all the while keeping the total optical thickness ˝ wave at the design kv0
2, The Incident medium index of refraction.
3. The High layer index of refraction
4. The Low layer index of refraction
5.The Substrate index of refraction
6.The angle of incidence in the Incident
medium
7. The number of layer pairs (half waves at the design
wavelength)
Finally, there is a Checkbox labeled “1/2 wave at center” that changes the optical thickness of the most central Low index layer to ˝ wave. This turns the stack which is normally a mirror at kv/kv0 =1 into a narrow band transmission filter as seen in Figure 3. As such it causes the E2max of the black trace to become very much greater than 1.
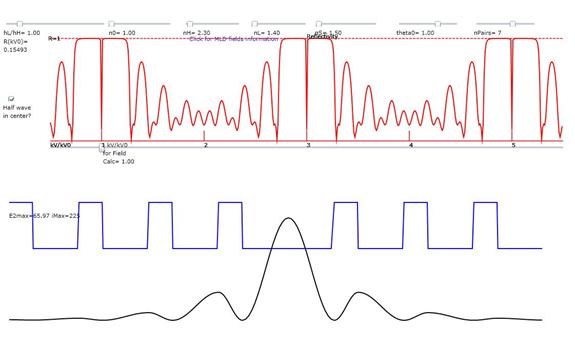
Figure 3: Fields and Reflection Vs kv/lv0 when the Half wave Checkbox at the left is checked. Note that the most central Low index layer is
now ˝ wave (twice as thick as the other Low index layers). Also note that the field intensity E2max is
very large in this ˝ wave layer. Note
too, from the red trace, that the reflection coefficient is nearly zero at
kv/kv0=1, 3, and 5.
Appendix
Comparison of quantum and acoustic wave behavior with that of electromagnetic waves
Introduction
It is often shown that the equations for reflection of quantum and elastic waves from an interface between two media have the same form as those for optical or electromagnetic (em) waves. For quantum waves, the requirement is that both the total wave amplitude and its first derivative must be continuous across the interface. It will turn out, as will be shown below, that the requirements for the E and H components of the electromagnetic are also that their amplitudes and their first derivatives must be continuous. The same will also be shown to be true for acoustic wave amplitudes and their first derivatives.
The reason for going through this exercise, is that, when we have
worked out the em field distribution for a complex dielectric layer
distribution, we will recognize that a similar distribution will also be valid
for the quantum and acoustic wave amplitudes with a simple change to the
quantum and acoustic analogues of the index of refraction of the layers.
In the following only normal
incidence of the waves on the interface will be discussed.
Quantum Amplitudes
For an interface that results in a change in potential energy of a quantum particle (like an electron) the quantum requirements are:
1. The total (incident+reflected+transmitted) amplitudes must be continuous. This means that particle probability density cannot have a step change.
2. The total first derivatives of the above amplitudes must be continuous. Since the first derivative represents the momentum of the particle, this means that the total momentum must not change across the interface.
The effective index of refraction (n) for a particle of incident kinetic energy, E, in a potential V is:
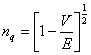
nq is real for V<E and totally imaginary for V>E. In that way, the effect of quantum potential distributions differ from the effect on em waves of dielectric layer distribution. Dielectric (and even metal) layers generally have indices of refraction that have both real and imaginary parts, albeit dielectric layers’ indices usually have very small imaginary components.
Because the effective index of refraction of potential layers can be imaginary, we must confine the comparison of results of quantum waves with em waves to cases where the quantum particle has energy E>V as well as to cases where V is negative.
Em Amplitudes
For em waves, the boundary conditions are derived from both the electric field, E, and the magnetic field, H, having the requirement that their components tangential to the interface be continuous. It is my task to show that this implies that the amplitudes as well as their first derivatives be continuous across the interface. For this purpose we will assume normal incidence along the x direction with the interface in the yz plane. For such a plane wave, Maxwell’s equations give:
![]()
and
![]() (1)
(1)
![]() (2)
(2)
![]() (3)
(3)
![]() (4)
(4)
Equation 2 shows that, if Hz is continuous, then the first derivative of Ey, as well as Ey, must also be continuous. Equation 1 shows that, if Ey is continuous, then the first derivative of Hz, as well as Hz, must also be continuous. Similar statements apply for Ez and Hy.
Therefore, the boundary conditions on the tangential components of E and H are the same as those for quantum wave amplitudes, even though E and H are polarized waves.
Elastic Wave Amplitudes
Elastic wave boundary conditions at a boundary between a two media that support shear stress are given in Reference 2[2]. They dictate that both the stresses and the displacements at the boundary be continuous. Since stress is proportional to strain (albeit in a complex way) and strain is proportional the first derivative of the displacement, this again requires that both the displacement amplitudes and their first derivatives are continuous across an interface between two media.
These results imply that the results for elastic wave amplitudes in layered media can also be inferred from the results for em wave amplitudes, although, as Reference 1 indicates, there is a greater variety of elastic wave types and the ratios of these types can be changed in the process of reflection and transmission.
The effective index of refraction of the elastic medium is
proportional to the inverse of the wave speed, be it a shear wave or a
compressional (longitudinal) wave and these speeds are given in Reference 2 as
equation 5.