Sublimation and Deposition

Introduction

Sublimation and Deposition are complex molecular phenomena. A good animation of these reversible processes is essential to their understanding. The animation discussed here will provide that understanding.

Figures

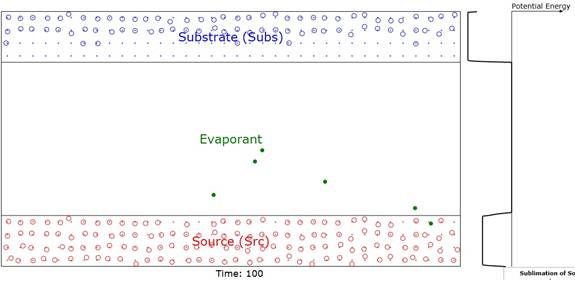
Figure 1: Showing surface barriers (potentials) and liquid, gas and solid phases color coded to be red, green, and blue. Note that some of the red molecules have evaporated (shown as green) into the space

between the Source and Substrate domains and are therefore candidates for deposition on the latter.

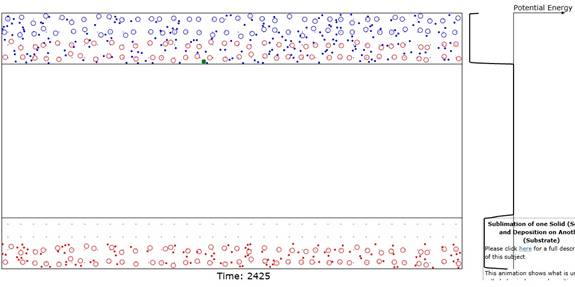
Figure 2: Showing result when coating (bottom 2 red layers) on Substrate is complete. Note that the top 2 Source layers are gone and only the red lattice anchor sites of these rows are visible in this Figure.

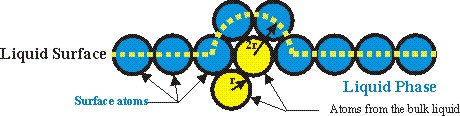
Figure 3. Figure related to Reference 1 showing the the heat of vaporization is a fairly simple function of the product of the surface tension and the area of a displaced hemisphere through which the centers of atoms pass at the surface of a liquid or solid.

Physics of Evaporation and Condensation[1]

All atoms or molecules have critical energies, E_e, above which they can exit the liquid or solid domain in which they are presently bound and enter the gas phase (evaporate) outside that domain. As shown in Reference 1, this energy is directly proportional to the surface tension (or, equivalently, the surface energy) of the surface of the particular liquid or solid in question (see Figure 3). Similarly all atoms or molecules in a gaseous state have critical energies, E_c, below which they may condense or dissolve into a neighboring liquid or solid surface or volume. Gaseous atoms with energy higher than E_c just reflect off the interface between the media. Since total energy in a closed system is conserved, the energy that a atom loses evaporating from the liquid or solid state is regained when it is condensed back into the liquid or solid state. In physics we call the energy needed for evaporation the potential barrier energy. An atom that has just been evaporated loses the potential barrier energy which is a substantial fraction of its kinetic energy while an atom that has just been condensed gains back a similar kinetic energy. So recently condensed atoms are "hot" but that extra kinetic energy is quickly dissipated via scattering with the cooler atoms of the liquid or solid. The animation permits adjustment of the potential energies as well as the average energies of the liquid, gas, and solid domains.

Evaporative Cooling

It's not so obvious from what has just been discussed, but when an atom has enough energy to evaporate, it carries a substantial fraction of its native media's energy with it. Since the atomic kinetic energy distribution is an exponential

$N (E) = N_{0} \exp (\frac{- E}{k T})$

and the total energy greater than E_c is given by ratio of the integrals:

$\int_{x_{1}}^{\infty} x \exp (- c x) d x = {\frac{\exp (- c x)}{c^{2}} (- c x - 1) |}_{x_{1}}^{\infty} = \frac{\exp (- c x_{1 `})}{c^{2}} (c x_{1} + 1)$

$\int_{x_{1}}^{\infty} \exp (- c x) d x = - {\frac{\exp (- c x)}{c} |}_{x_{1}}^{\infty} = \frac{\exp (- c x_{1})}{c}$

$\frac{\int_{x_{1}}^{\infty} x \exp (- c x) d x}{\int_{x_{1}}^{\infty} \exp (- c x) d x} = \frac{1}{c} (c x_{1} + 1)$

where c=1/kT and E_c =x₁. Note that the average energy of the entire energy range is kT.

Then only those atoms with E>E_c can evaporate, the change in average energy is:

$E = \frac{\int_{0}^{\infty} E \exp (\frac{- E}{k T}) d E}{\int_{0}^{\infty} \exp (\frac{- E}{k T}) d E} - \frac{\int_{E_{c}}^{\infty} E \exp (\frac{- E}{k T}) d E}{\int_{E_{c}}^{\infty} \exp (\frac{- E}{k T}) d E} = k T (1 - (E_{c} / k T + 1)) = - E_{c}$

which is essentially the average energy of all the atoms with energy above E_d. Thus, on average, when an atom evaporates, it reduces the energy of the entire atomic ensemble by:

$< Δ E > = - E_{c}$

The total loss of energy when a large group, N_e, of atoms evaporates is of course

$Δ E_{N e} = - N_{e} E_{c}$

Solving for the final temperature, T_f, and taking the differential we have

$\begin{array}{l} E_{i} = N_{i} k T_{i} \\ E_{f} = (N_{i} - N_{e}) k T_{f} = N_{i} k T_{i} - N_{e} E_{c} \\ T_{f} = \frac{N_{i} k T_{i} - N_{e} E_{c}}{(N_{i} - N_{e}) k} \approx T_{i} - \frac{N_{e} E_{c}}{N_{i} k} \\ Δ T = T_{f} - T_{i} \approx - \frac{N_{e} E_{c}}{N_{i} k} \end{array}$

where the approximation is valid when N_i>>N_e.

Another way of expressing this equation is to compute the heat energy of evaporation, Q, per gram molecular weight, n, evaporated:

$Q = - n A E_{c}$

where A is Avogadro's number.

Specifics of Sublimation and Deposition

In this discussion, the Source and Substrate solids are made up what will be called ions and electrons. The ions vibrate around fixed uniformly spaced anchor points in the solids. The electrons are free to range over the entire domain of the solid and they regularly collide with the ions, exchanging energy with them. Since the electrons receive some energy from one ion and give some energy to another ion, this provides a way of coupling the ions.

The ions have to have more than a certain critical energy climb the potential hill at the surface of the solid and thereby to escape their host and become vapor atoms. This is called the enthalpy of evaporation. On the other hand, one might think that vapor atoms would always be deposited on the subs since they only have to drop down the potential hill at its surface. That concept, however, does not take into account the fact that the vapor atom undergoes collisions with the atoms at the surface of the Substrate. If the kinetic energy of the vapor atoms is too large and/or the direction of the nearest subs ion is outward from the surface, the vapor atoms just recoil from the surface rather than being deposited on it. This process has the effect of compacting the coating which is usually a good thing but does not further increase the thickness of the coating. None of these recoils are illustrated since they're beyond the scope of this animation but the viewer needs to understand that they happen on regular basis.