Physics and Math of Swing Pumping

Introduction

A child pumping (increasing amplitude) of a swing is a well known example of the way that the amplitude of a harmonic oscillator can be increased. It is important that the extra force be applied during the middle of the swing. Also, in order to increase the total energy of the swing, the child must act against both gravity and centripetal force.

Math and Physics

One of the more obvious behaviors in swing pumping is that the child lifts her/his lower legs so that the shins are parallel with the thighs while the swing is going forward and lets them return to 90 degrees with respect to the thighs while the swing returns. The act of lifting the lower legs at the bottom of the swing trajectory and returning them at the top has the effect of adding gravitational energy to the total energy of the swing. Let the mass of the lower legs be named m_L and their length be named L_l . The energy added to the swing by this act alone is then

(1)

where the effective height the legs are raised is L/2 and g is the acceleration of gravity. At any one time, the total energy of the swing is

(2)

where M is the mass of the child, L_s is the length of the swing rope, and t_Amp is the angle of maximum amplitude of the swing.

Equation 2 can be solved for the maximum swing angle:

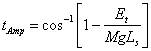(3)

We can solve equation 3 for the change in amplitude per unit energy input via pumping:

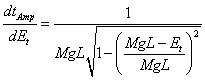(4)

We can then use this derivative with equation 1 to find the change in amplitude per swing:

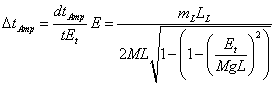(5)

We see from equation 5 that the amplitude added per swing period is somewhat larger than ½ of the mass times length ratio.

As a numerical example take the following values:

M_L=5 kg

L_L =0.3 m

L=2.5 m

M=30 kg

t_Amp=0.5 radians

Then

E_t=90 Joules

Then:

Dt_Amp=0.014 radians per swing period.