Taylor and Wheeler Lorentz Derivation

Prologue

The Taylor and Wheeler derivation relies entirely on the velocity invariance of the space time interval between two events. This invariance is usually shown by a kinematics diagram where a light signal is emitted in a direction perpendicular to the usual direction of motion such as in Figure 1.

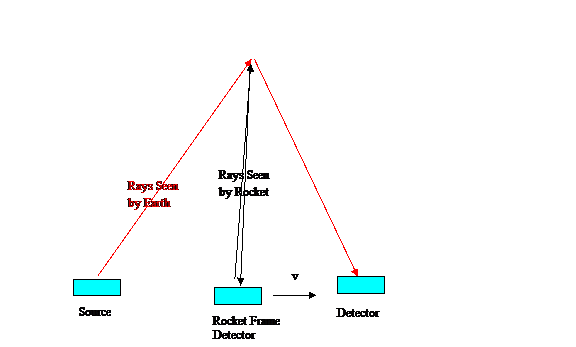
Figure 1: Kinematics diagram of the light pulses used to show that the space time interval between emission and detection is the same whether in the rocket frame moving at speed v or for a stationary earth observer.

The space-time quantity called the invariant (with respect to the observer's frame of reference) interval between two events is the expression

$δ s^{2} = c^{2} δ t^{2} (v) - δ x^{2} (v)$

(1.1)

that, strangely, does not depend independently on the value of $δ x$ because $c δ t$ changes just enough to compensate for the change in $δ x$ . The kinematics of this become obvious when we draw a diagram of the emission, reflection, and reception of a light pulse which travels in a direction perpendicular to the x axis while the motion of the primed coordinate system is parallel to the x axis.

What I'd like to do is the re-write the interval in terms of the electromagnetic quantities that really constitute the speed of light squared, $μ$ and $ε$ . Then the interval equation (1.1) becomes

$δ s_{t}^{2} = δ t^{2} (v) - (μ ε) δ x^{2} (v)$

(1.2)

where, for the time being, I have chosen to remove the zero subscripts from $μ$ and $ε$ so that the expression applies to a material body as well as vacuum. This equation demands that space and time between two events are inextricably bound together regardless of the speed of the observer and the coefficient of the binding just happens to be $\sqrt{μ ε}$ which happens to be 1/c². If we, in the first place, had postulated that equation (1.2) holds regardless of the motion of the observer, we could have avoided the kinematics diagrams that lead to it.

Let's take the simplest case where the one reference frame is inside the rocket so the speed in that frame is zero then in that frame $δ x = 0$ :

$δ s_{t}^{2} (0) = δ t^{2} (0)$

(1.3)

Then relative to this interval any other interval will be the same so we can solve for $δ t_{}^{2} (v)$

$\begin{array}{l} δ t^{2} (v) - (μ ε) δ x^{2} (v) \equiv δ t^{2} (0) \\ δ t^{2} (v) = δ t^{2} (0) + (μ ε) δ x^{2} (v) \end{array}$

(1.4)

Since no transformation is required, it is very easy to determine $δ t_{}^{2} (0)$ , so equation (1.4) gives us a very simple way to get a numerical value of $δ t_{t}^{2} (v)$ if we know $δ x_{}^{2} (v)$ .

Deriving The Lorentz Transformations from The Invariant Interval

They take the case of the pi meson from the upper atmosphere whose lifetime is extended by a large factor by its speed. The two events are the birth and death of the pi meson. The distance between these events is

$x = v t$

(1.7)

where t is the time between events and v is the speed of the pi meson after birth. Taking the interval between the events we have

$s^{2} = c^{2} t^{2} - x^{2} = c^{2} t^{2} - {(v)}^{2} t^{2} = c^{2} t'^{2} - x'^{2}$

(1.8)

where t' and x' are the time and position in the meson inertial frame and the intervals are the same in both frames. Of course the value of x' is always 0 in the meson frame and the time between birth and death, t', in the meson frame is t_π which is about 8 nanoseconds. Now we can solve for the value of t.

$t = \frac{t_{π}}{\sqrt{1 - {(v / c)}^{2}}}$

(1.9)

and then we also have

$x = \frac{v t_{π}}{\sqrt{1 - {(v / c)}^{2}}}$

(1.10)

Note that the most fundamental concept used here is the invariance of the interval which, in turn, relies on the fact that the speed of light is the same in all inertial frames of reference.

The simple way of deriving the invariance of the interval is to set up a clock on a rocket where light pulses are sent along the y axis in the rocket frame to a mirror at a given distance from the rocket and then received. The lab frame's time interval between sending and reception is different from that of the rocket but the interval between sending and reception is the same in both frames.

The foregoing is a rather special case in that x'=0. Let's now generalize this to cases where x' can be any value. We can write equations (1.9) and (1.10) to include both t' and x'.

$\begin{array}{l} c t = \frac{c t'}{\sqrt{1 - {(v / c)}^{2}}} + A x' \\ x = \frac{v t'}{\sqrt{1 - {(v / c)}^{2}}} + B x' \end{array}$

(1.11)

Again require that the interval in both frames be the same:

$c^{2} t^{2} - x^{2} = c^{2} t'^{2} - x'^{2}$

(1.12)

$\begin{array}{l} c^{2} t^{2} - x^{2} = \\ {(\frac{c t'^{}}{\sqrt{1 - {(v / c)}^{2}}} + A x')}^{2} - {(\frac{v t'}{\sqrt{1 - {(v / c)}^{2}}} + B x')}^{2} \\ = \frac{c^{2} t'^{2}}{1 - {(v / c)}^{2}} + \frac{2 c A t' x'}{\sqrt{1 - {(v / c)}^{2}}} + A^{2} x'^{2} - (\frac{v^{2} t'^{2}}{1 - {(v / c)}^{2}} + \frac{2 B v t' x'}{\sqrt{1 - {(v / c)}^{2}}} + B^{2} x'^{2}) = c^{2} t'^{2} - x'^{2} \end{array}$

(1.13)

Collecting t'² terms we have a simpler equation:

$c^{2} t^{2} - x^{2} = c^{2} t'^{2} + \frac{2 c A t' x'}{\sqrt{1 - {(v / c)}^{2}}} + A^{2} x'^{2} - (\frac{2 B v t' x'}{\sqrt{1 - {(v / c)}^{2}}} + B^{2} x'^{2}) = c^{2} t'^{2} - x'^{2}$

(1.14)

which means that the remaining x' terms on the left must equal -x'².

$\frac{2 c A t' x'}{\sqrt{1 - {(v / c)}^{2}}} + A^{2} x'^{2} - (\frac{2 B v t' x'}{\sqrt{1 - {(v / c)}^{2}}} + B^{2} x'^{2}) = - x'^{2}$

(1.15)

Obviously the cross term in t'x' must be zero so

$A = (v / c) B$

(1.16)

And we also have the condition that

$\begin{array}{l} A^{2} - B^{2} = - 1 \\ [^{(v / c) B] 2} - B^{2} = - 1 \\ B = \frac{1}{\sqrt{1 - {(v / c)}^{2}}} \\ A = \frac{v / c}{\sqrt{1 - {(v / c)}^{2}}} \end{array}$

(1.17)

Using these results we write the final expressions for equation (1.11)

$\begin{array}{l} c t = \frac{c t'}{\sqrt{1 - {(v / c)}^{2}}} + \frac{(v / c) x'}{\sqrt{1 - {(v / c)}^{2}}} \\ x = \frac{v t'}{\sqrt{1 - {(v / c)}^{2}}} + \frac{x'}{\sqrt{1 - {(v / c)}^{2}}} \end{array}$

(1.18)