The thin lens approximation

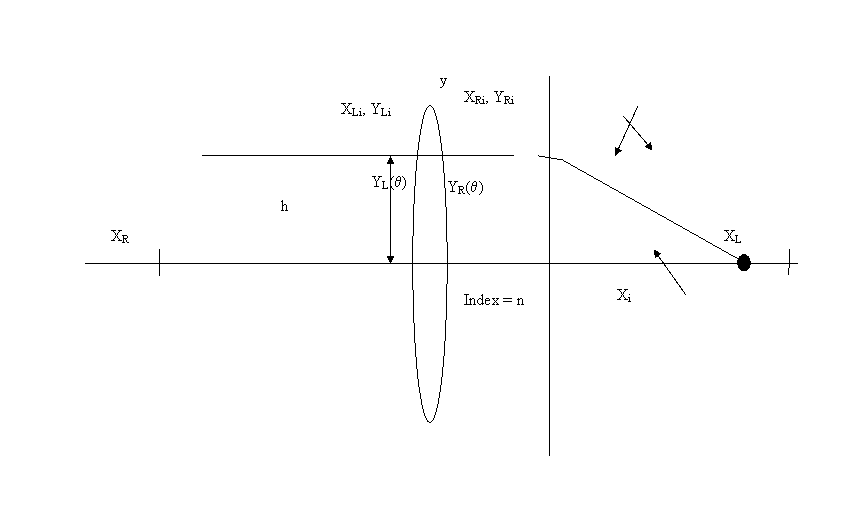
1. Derivation of the thin lens focal length

To derive the thin lens approximation for the focal length we have to assume that all angles are small so that the following approximations hold:

where all angles herein are expressed in radians.

The angle of interception of the ray at height h relative to the normal of the left surface of the lens is:

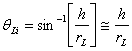
The angle of refraction at the left surface is given by Snell’s law as:

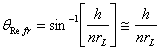
and this results in the following slope relative to the x axis for the refracted ray:

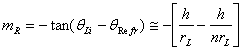, a negative number.

At this point we ignore the thickness of the lens at height h and concentrate on computing the refraction angle on the right surface of the lens.

The height of the ray at the right surface is then also h and the angle of the surface normal relative to the x axis there is.

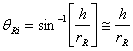
Relative to this surface normal the incidence angle on the right surface of the lens is

The refracted angle is then n times this angle:

The angle of this ray relative to the x axis is obtained by subtracting off the angle of the surface normal:

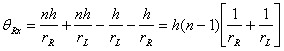
and this corresponds to a negative slope.

An equation for y with this slope starting at h is:

The distance from the height h until this negatively sloped line crosses the x axis is defined as the focal length, f, and is:

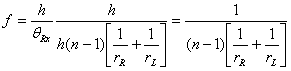
The fraction on the right side of the equation is the standard expression for the focal length of a thin lens.

2. Derivation of the thin lens equation for the image distance

The standard ray drawing is as shown above. A paraxial ray, R_p, that arrives at the lens from the Object arrow head is refracted so that it passes through the focal point at distance f from the lens. Another ray, R_c, passes through the area center of the lens, is un-deflected, and intersects with the previous ray at the head of the Image arrow. Our task is to compute the image distance, i, in terms of the object distance, o, and the focal length f.

We can immediately note that the following equations apply:

R_p:

R_c:

We wish to know the x value of the intersection of these two rays and therefore we set:

Solving for x_i results in:

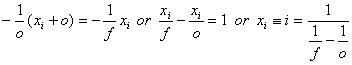
We may divide both sides of this expression into 1 and obtain

and re-arranging by adding 1/o to both sides we have:

This is the standard form of the thin lens expression that relates the image and object distance to the focal length.

From the drawing it is obvious that the magnification, M, is:

since the triangles having R_c as hypotenuse are similar.