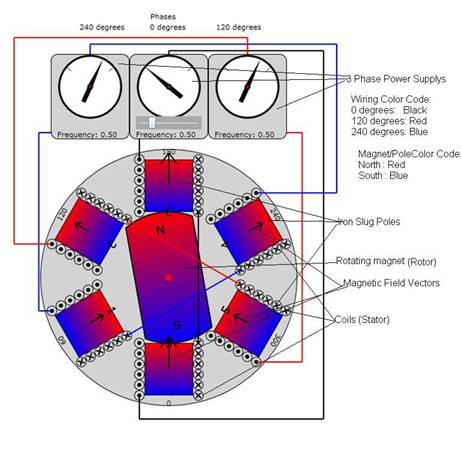
Three Phase Motor
Introduction
There is no doubt that an electric motor is a complex system of magnets and magnetic fields. It is the intent of this animation to show explicitly how a three phase alternating current (AC) motor is driven.
Explanations of Graphics
Figure 1: Diagram of the animated motor. It is important to understand that the view
I’m showing here is a cross-section.
Often, the depth of the motor into the screen is much larger than its
diameter. Besides the information already noted on the Figure, you should
understand that a cross inside the wire cross section means that the current is
going into the screen and a dot inside the wire means that the current is
exiting the screen. The direction of the
current determines the direction of the pole’s magnetic field. The phase angles
of the poles are clearly labeled 0-360 and the magnetic field vectors, B, are
shown scaled to length depending on current supplied to the particular pole.
When running the animation, note that the long magnetic field
vectors rotate clockwise with the rotating permanent magnet. A three phase motor has the reputation that
it is a “rotating magnetic field” device.
You can see that the permanent magnet usually lags this rotating
magnetic field.
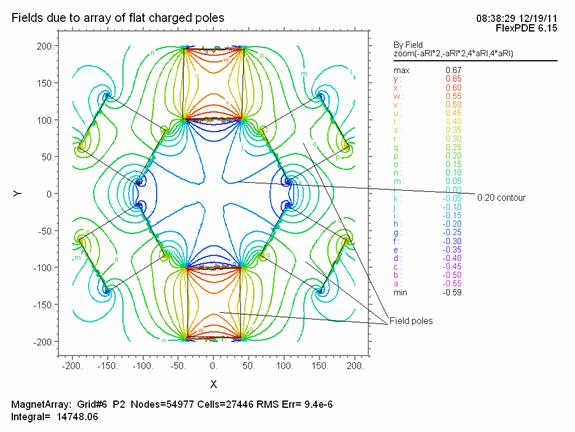
Figure 2: Contour plot of the vertical component of
the magnetic fields, By, due to the 6 coils in Figure
1 where the top and bottom pole pieces had fields of -1.0. The units of the By
fields units are relative. Note that, at the center of the coil array, the
field is approximately -0.17.
The magnet field contour plot in Figure 2 is based on the having unity field at the top and bottom poles and cosine of 60 degrees (or half unity) fields on the other as would be the case when the 0 degree generator is peaked while the 120 degree and 240 degree generators are at half peak.
In the actual animation, when the
torque on the permanent magnet is computed, it is assumed for simplicity only that
the vector sum at the center of the pole array can be as large as the sum of
all the fields on the pole which, in this case would be
1+1+1/2+1/2+1/2+1/2=4. Of course, the
actual torque on a permanent magnet of practical size would not be proportional
to the magnetic field at the center of the array but instead would be related
to the magnetic field values at the north and south poles of the permanent
magnet when these poles are near the coil poles of the array.
Calculations
The actual magnetic fields shown in Figure 2 are a complex function of the sizes and magnetic permeability of the pole pieces as well as the number of wire turns of each coil. For each coil, the axial magnetic induction, B, inside the coil is given approximately by the standard formula for solenoids:
![]() (1)
(1)
where m0=4px10-7 Newton Amp-2, N is the number of wire turns, i is the current, L is the axial length of the coil, B is in units of Weber meter-2 or Tesla and the magnetic field strength, H, is defined implicitly as Ni/L. The addition of an iron slug somewhat increases the internal axial B, but not by a factor as large as the slug’s relative permeability.
Having computed the coil array’s total magnetic field, one can use the following equation to compute the torque on the permanent magnet:
![]() (2)
(2)
where the vector m is the magnetic dipole moment of the permanent magnet and the x between m and B indicates the cross product. To define m we use the value of the magnetization, M which is defined as:
![]() (3)
(3)
In air, where m=m0, H=B/m0 so M=0 as one might expect.
The actual equation for computing the dipole moment of a permanent magnet of uniform magnetization M is:
![]() (4)
(4)
dv is the volume element and the integration is over the volume of the magnet. While equation 2 would be correct for a very small magnet occupying the center of the pole array in Figure 2 and, at that location, the pole-induced magnetic field rotates uniformly, because of equation 4, such a motor couldn’t produce much torque or power. Early motors used rotors whose radii where much less than the internal radius of the pole array. Then it was discovered that having a very small gap between the rotor and stator was essential to motor performance. To simulate the behavior of the motor in an intuitive manner, we will use the concept of a uniform magnetic charge, qM, on the ends of the iron slugs as well as on the ends of the permanent magnet. For a very high permeability iron slug, the value of qM is given by:
![]() (5)
(5)
and make the assumption that qM will be uniform across the pole faces. The
variation of the stator pole magnetization charge, qM, with coil input current is shown as a
change of diameter of the individual charges on the end faces.
With the charge concept we are led to the following 3 Figures.
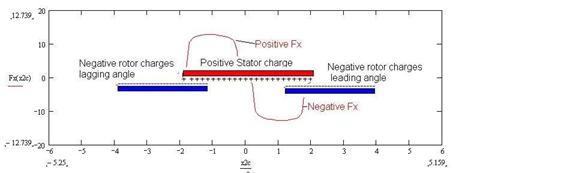
Figure 3: Forces between two charged plates that are
closely spaced along the vertical direction.
The blue negatively charged plate’s horizontal position is variable and
it simulates the rotor in the 3 phase motor.
It is shown in two positions: 1 With its right
edge adjacent to the left edge of the red positively charged plate (stator) and
2. With its
left edge adjacent to the right edge of the stator. Of course, the force in the x direction is
positive (as shown) in position 1 and negative in position 2. As shown, it is obvious that there will be no
net average force as the blue plate makes a long passage from left to right
under the red plate.
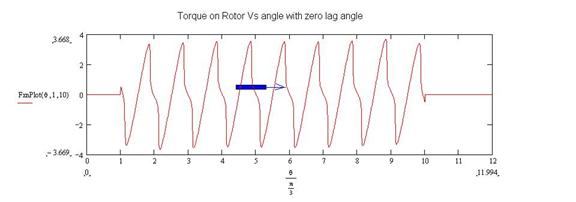
Figure 4: Forces between charged plates that are
closely spaced along the vertical direction.
. The blue negatively charged
plate’s horizontal position is variable and it simulates the rotor in the 3
phase motor. The force is shown as it sequentially passes 9 stator poles. In this case there is no lag angle between
the rotor passage and the peak charging of the adjacent stator pole of about 15
degrees. As a result there is zero net
average force in the positive x or clockwise direction.
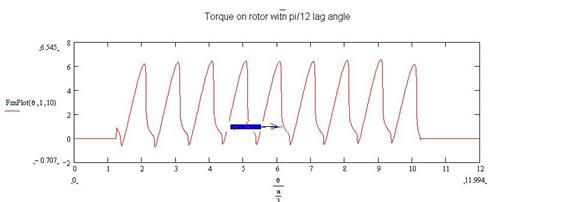
Figure 5: Forces (or torque) between charged plates
that are closely spaced along the vertical direction. . The
blue negatively charged plate’s horizontal position is variable and it
simulates the rotor in the 3 phase motor. The force is shown as it sequentially
passes 9 stator poles. In this case
there is 15 degree lag angle between the rotor passage and the peak charging of
the adjacent stator. As a result the
torque is positive (clockwise) at almost all angles.
The previous 3 Figures show the variation with position or angle of the forces induced on the rotor pole by the stators. In Figure 3, there is no variation of the stator current as the rotor passes under it and therefore there is no net force. In Figure 5 there is a variation of the stator current during the passage of the rotor under the poles and therefore there is a net average clockwise force on the rotor.
All of this can be seen dynamically in the actual animation along with a plot of the torque Vs time and the torque sum versus time.
This brings us to another reality of brushless motors: their speed is not uniform. The equation for angular acceleration of the permanent magnet as well as any loads that are attached to it is:
![]() (6)
(6)
where I is the moment of inertia of the rotor plus any loads attached to it, w is the angular speed of the rotor, and t(t) is the torque applied by the interaction of the rotor with the stators.
An alternative (and more useful for this case) expression of equation 6, not involving time, is:
![]() (6a)
(6a)
where q is the rotor angle.
In general t(q) is a periodic function of rotor angle so w will also be a periodic function of q. Then the incremental variation of w with respect to q will be:
![]() (6b)
(6b)
where dq is the rotor’s incremental rotation angle. Another way of solving equation 6a is to integrate both sides with respect to q
 (6c)
(6c)
which is just a statement of the conservation of rotational energy. In general the lower limits of the integrals are not zero because we assume a starting value of w0, so the equation above becomes
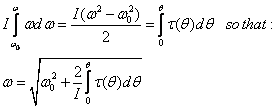 (7)
(7)
The average value, w0, of w is defined by the ratio of the power output to the average torque:
![]() (8)
(8)
where <P> is the average power being used in the mechanical load. Also, here we can make the definition
![]()
where L0 is the average
angular momentum.
Since there are 6 stator pole encounters per rotor revolution, we know that the speed will be modulated 6 times per rotation of the rotor. Thus, as an algebraic example, we make the assumption that the torque is sinusoidal with time:
![]()
where dt is half of the peak to peak variation of t and f is a phase lag factor. Then we can integrate the expression in equation 7 to obtain:
![]()
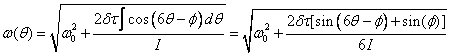 (9)
(9)
Because of equation 9 we expect the rotational speed of the rotor to vary periodically as it passes stator poles and that is indeed shown in the animation.
As a numerical example, I propose the following quantities:
Frequency f=1 Hz (w0=2p)
Inertial Moment I=0.1 kg-m2
Peak Torque deviation : 5 Newton-meter
Then equation 9 yields:
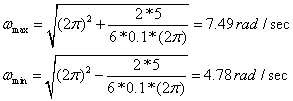
so that the rotational frequency varies from 0.76 Hz to 1.21 Hz under these conditions.
To actually implement computing the rotational speed, we need to compute the integral in equation 9 numerically. We do this by saving the torque values in an array T[i]. Then we sum the array up to the current value, n, and take the average thusly:
![]()
where N corresponds to very many
revolutions of the rotor.
Then equation 9 becomes:
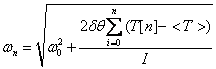
where dq is the angle step size.