The Relativistic Twin Paradox Using Segmented Speeds
Introduction
The problem with most treatments of the twin paradox is that they don’t take into account that both the “moving” and the “stationary” twins see their sibling’s clocks moving at the same (slower) rate than their clock and therefore might conclude that their ages at the end of an out and back trip should be the same. Of course, it is well established experimentally that, after an extended trip by one of the twins, that twin will come back younger than his stay-at-home sibling. That leads to the concept that the difference in age must occur during the traveling twin’s acceleration due to firing his retrorockets to return to earth. It is well known that acceleration has the same effect as an artificial gravity and we all know that light emitted from atoms in large gravitational fields (like black holes) has its frequency reduced (is red-shifted).
Calculations
First let’s just compute the difference in age that one might expect the twins to have if:
- We didn’t take into account the fact that one twin was accelerated and the other was not.
- We just compute the difference between the stationary twin’s time observed on his own clock, Tss, and the time Tst observed by the stationary on the traveling twin’s clock.
- The duration, Tc=Tss, of the cruise portion of the flight is much longer than the turn-around duration, Ta.
From the time dilation equation we have:

The expected time difference at the end of the trip is then approximately:
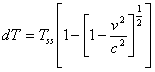
It is this time, dT, that must be made up during the retro-rocket turnaround time Ta. Therefore the stationary twin’s clock must speed up by a factor r that is greater than 1 while the accelerated twin’s clock must slow down by the factor 1/r.
That results in the equation:
![]()
Which we can solve for r and obtain:
![]()
where the latter approximation is valid for the case Tc>>Ta.