Precession of a Top
Introduction
A
precessing mechanical top is a good prelude to understanding the effects of a
magnetic field on electrons and nucleons in atoms. The animation that this document describes
should give the learner some hands-on experience with that precession,
Figures
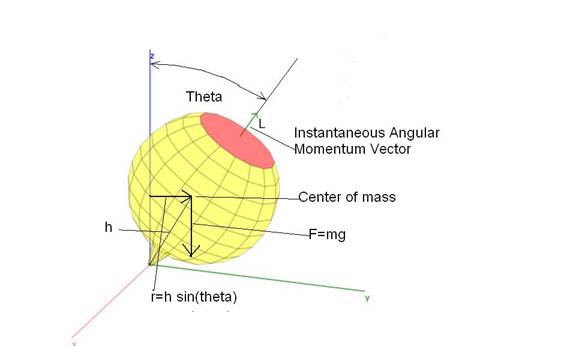
Figure 1: The top precesses about the z axis at angle q. The diagram
shows the instantaneous angular momentum vector, L, as well as the center of
mass. The force, F=mg, is that due to
gravity. This force provides toque at
radius r=h sin(q) where h is
the height of the center of mass above the x-y plane when the top is aligned
with the z axis.
Calculations
In steady precession the angular momentum can be described as:
![]() (1)
(1)
where the bold x and y are unit vectors in the x and y directions, respectively, q is the tilt angle with respect to the z axis and w is the angular rate of precession.
The torque, t, that causes the precession has to be synchronous with L and is:
![]() (2)
(2)
And the pertinent equation relating the precession to the torque is:
![]() (3)
(3)
From equation 3 we easily obtain the angular rate of precession as:
![]() (4)
(4)
Summary
Note that the precession frequency is independent of the
angle of tilt because both the torque and dL/dt are proportional to the sine of
the tilt angle. As the top slows down,
however, L0 decreases, increasing the rate of precession and the
tilt will become larger until finally it will lie on the floor.