Transformer with a Resistive Load

Introduction

A transformer is an important device in the real world because of the following features:

1. It can increase or decrease the alternating current voltage levels to drive loads that require different voltages.

2. It provides electrical isolation between the primary (driving) side and the secondary (driven) side.

3. Without much extra effort there can be more than one secondary winding added to provide voltages to several different devices.

In this animation, we will show the magnitudes and phases of the currents in the primary and secondary circuit.

Calculations

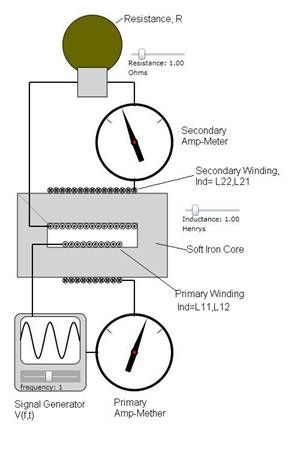
Figure 1: diagram of the circuit being analyzed and animated.

As shown above we have 2 circuits. There is a primary circuit with a signal generator (AC voltage supply, V(t) with variable frequency, f) and the primary winding with inductance L₁₁ and mutual inductance L₁₂. The secondary circuit has a winding with inductance L₂₂ and mutual inductance L₂₁ as well as a resistor, R.

Since there is no charge sink such as a capacitor for this diagram, we do not need to keep track of the charge. Only the current and voltages across the inductances, resistor and signal generator need to be computed.

The appropriate equation for the primary circuit is:

(1)

where f is the source frequency, i₁ and i₂ are the currents in the primary and secondary circuits and I have assumed that the signal generator is a perfect voltage source with peak voltage V_p. For compactness of notation, we will henceforth use the radian frequency w=2pf.

A similar equation for the secondary circuit is:

(2)

where R is the resistance of the light bulb.

We solve equations 1 and 2 in exactly the same way as was used for the Driven LCR Oscillator. Let the applied voltage be shown as

and then let the solutions for the currents be stated as the real parts of the following equations:

where i (without the subscript) is the square root of -1 and both I₁ and I₂ are complex. With these substitutions we can write equations 1 and 2 as:

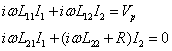(3)

In shorthand notation, the inverse of the coefficient matrix of I₁ and I₂ is:

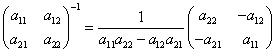(4)

where:

(5)

Therefore the solutions for I₁ and I₂ are:

(6)

In more explicit terms the solutions are:

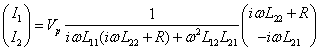(7)

Our next task is to separate the real and imaginary parts of I₁ and I_2.

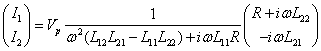(8)

Equation 8 is of the form:

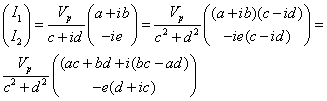(9)

where:

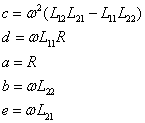(10)

where now the real and imaginary parts are explicitly separated and the analogy with the quantities in equation 8 are obvious. The magnitudes of the currents in equation 8 are:

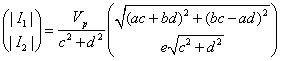(11)

while the phases of the currents are:

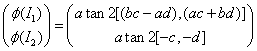(12)

where the function atan2() evaluates the arctangent smoothly over the domain -p->p.

Summary

Because, with the iron loop core, the magnetic flux, F, and its variation with time, dF/dt, are essentially the same in both the region of the primary coil and secondary coil. But since the secondary number of turns, N_s, is different from the primary number of turns, N_p, we expect that the voltage across the secondary will be in the ratio N_s/N_p to that across the primary, at least under conditions of a small load in the secondary.

Also, with the iron loop core, the mutual inductances, L₁₂ and L₂₁, are both proportional to N_sN_p while the self inductances are proportional to N_p² and N_s², respectively. If there is very small flux leakage, then the term c in equations 9 and 10 can be very small. In the event that the term c is zero then the secondary circuit current becomes

which essentially states that the effective voltage in the secondary circuit is N_s/N_p times that in the primary circuit.