Twin Paradox with Sinusoidal Speed Variation
Introduction
It has always seemed to me that the hardest part to swallow about the twin paradox is the “instantaneous” turnaround of the spaceship twin at his farthest distance from earth. The following treatment will analyze the total time observed by the spaceship twin when his speed profile is sinusoidal so that his turnaround(s) are smooth.
Equations
We will express the speed of light, c, in light years per year and designate a round trip that takes a total Tt=10 years (subscript t stands for trip). Of course, the distance traveled by the spaceship will be less than 10 light years because the ship’s speed varies sinusoidally as:
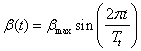
where, of course, the velocity, v, is:
![]()
We can determine the x coordinate at any time by integrating v(t):
![]()
where, for convenience, I have designated:
![]()
Obviously
![]()
so the total distance traveled is 6.36 light years.
The time observed by the space twin will be measured as the accumulated phase of a Doppler-shifted light wave she receives from earth. On earth the radian frequency, wc, (where subscript c stands for clock) of this signal is perfectly constant and the signal is expressed as
![]()
where E0 is the peak amplitude of the signal and, for better time resolution, we will assume that wc>>wt.
The space twin will see the frequency of the Earth signals
Doppler shifted by the factor:
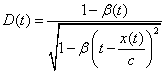
Here the b(t) in the numerator represents the effect of the space twin’s present speed with respect to the wave-fronts (signals) already present at his position x(t). The factor
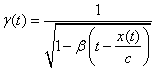
is the time-lagged Lorentz factor which represents the rate of the Earth clock as seen by the space twin at his present position.
The total phase that the space twin observes up to time t is
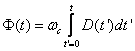
The following is a plot of both F(t) and wct Vs x(t):
![]()
![]()
![]()
![]()
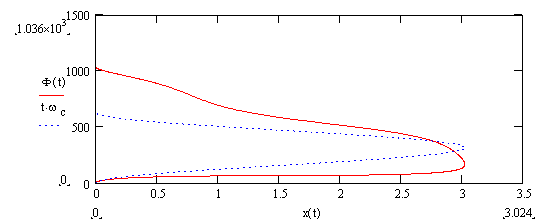
Figure 1:Phase accumulation
of a local clock(blue trace) and perceived phase accumulation of Earth clock as viewed from a space ship in
sinusoidal motion with a maximum speed of 0.95 c.
where wc was chosen so that earth emitted 10 cycles per
year and bmax was chosen as
0.95. The starting condition for both
the earth phase and the space phase is, of course, zero. Note that that blue trace is symmetric with
respect to outgoing and incoming phase accumulation. However, the red trace shows a dramatic
increase in phase accumulation about one half of the way through the trip and ¾
of the way through the trip. These
locations are where the denominator of D(t) is quite
small.
The
spaceship twin also has an clock identical to that of
the earth twin and its phase accumulation is thus necessarily given by the blue trace in Figure 1. So the
spaceship twin’s perception of the earth twin’s phase (or time) accumulation
ends up larger than his own local time accumulation.
Conclusions
Although somewhat more mathematical than the usual instant-turnaround space trip analyses, I think that this treatment is much more convincing than the other-because sudden coordinate frame jumps are just really hard to grasp-to me they’re similar to sleight of hand.
Some may argue that I haven’t
included the general relativistic effects of acceleration. With this
speed profile, I can at least state that the peak acceleration can be made as
small as desired simply by making the trip time longer.