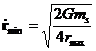Mathematics of Two Attracting Particles
General Setup
Note: Bold characters in equations denote vectors.
Central force law
![]()
We then use
![]()
where xi are the positions of the centers of the bodies.
R is the center of mass vector
Conservation of momentum:
![]()
Center of mass speed:
![]()
![]() since the second time derivative of R is zero.
since the second time derivative of R is zero.
Center of mass position vector:
![]()
where t=time.
Particle relative displacement r:
![]()
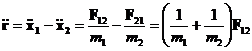
![]()
Reduced mass:
![]()
Mass sum:
![]()
Kepler Orbit Parameters:
http://en.wikipedia.org/wiki/Kepler_orbit
![]()
![]()
where G is the gravitational force constant
For the non-vector r acceleration, we must take centripetal acceleration into account:
![]() (1)
(1)
For gravitational forces:
Let:
![]() where
G is the gravitational constant
where
G is the gravitational constant
For charged particle forces.
![]()
where Z1 and Z2
are the charge numbers of the particles, e is the electronic charge, and e0 is the permittivity of
vacuum. The following Kepler orbit treatment will be valid only for particles of
opposite charge.
The specific angular momentum, H, is a signed constant pointing along the z direction:
![]()
where r0 and v0
are the starting values for r and v and
![]()
The speed transverse to r is:
![]()
Let s=1/r:
Then from equation 1 we can write the following differential equation for s:
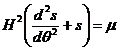
The solution for s is:
![]()
where q0 is the usually chosen to be 0 at the major axis.
![]()
If we let q-q0=0, then we can compute e in terms of the initial value, r0, of r:
![]()
If H is large enough, |e| can be larger than 1 and that will cause a hyperbolic orbit.
Speed parallel to r:
![]()
Define a speed associated with the constants of motion:
![]()
To choose reasonable initial values for r0 and v0,
see the Appendix.
We next obtain the initial angle using the above parameters:
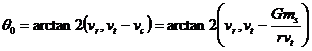
where arctan2(y,x) computes the value of q0 on the entire unit circle.
Orbit eccentricity e from above parameters:
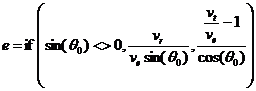
Note that e can be negative as used in this document.
Coordinate system unit vectors, x1,y1, of the major and minor axis of the ellipse:
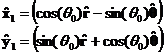
where the unit r and q vectors are defined in terms of the initial r as follows:
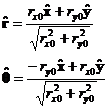
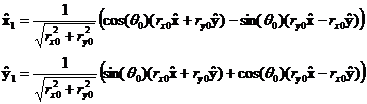
r(q)
can now be expressed in terms of q0
and qdot as:
![]()
where the rate of angle change:
![]()
We want to express the new vector r in terms of the x1 and y1 coordinate system so that at q=q0 the values r and r0 are the same. Obviously we can write the following vector expression for r any time t:
![]()
We only have to use the expressions for unit vectors x1,y1 to express r in terms of the original coordinate system.
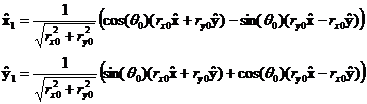
The inverse relations for x1 and x2 are computed below:
Repeating the expressions for R and r:
![]()
![]()
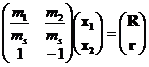
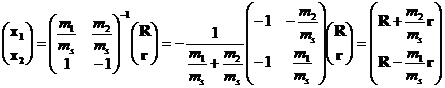
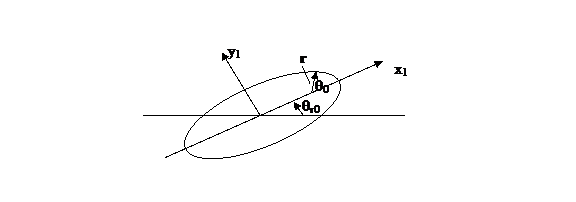
Figure 1: Diagram of the elliptical orbit of the
separation vector r showing the tilted
ellipse angle qr0 as well as
the angle of r in the elliptical
coordinate system .
The diagrams of the individual particles will be different.
The value of qr0:
![]()
Appendix: Finding the maximum relative velocity for an elliptical orbit of finite size:
Repeating the equation for the second time derivative of r:
![]() (A1)
(A1)
Rewrite A1 using the chain rule:
![]() (A2)
(A2)
Integrating both sides with respect to r we have:
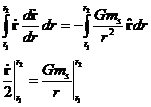 (A3)
(A3)
If we set r2 equal to infinity and relative velocity at r2 equal to zero then we can solve for the maximum allowable speed at r1:
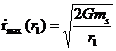
![]() (A4)
(A4)
The speed in this equation is often called the "escape
velocity" but is more accurately referred to as the escape speed since its
value doesn't depend on the direction of ![]() .
.
Equation A4 is useful conceptually but, for the animation
purposes, we can't allow r2 to be infinity. Therefore using equation A3 but this time
setting r2=rmax and ![]() =
=![]() we have a more useful expression for rmax :
we have a more useful expression for rmax :
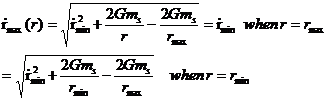
A reasonable choice for ![]() might be
might be