Derivation of Maxwell Energy Distribution in Multiple Dimensions
Introduction
This
animation shows how the 1, 2, 3 and 4 dimensional velocity (or speed) and
energy probability distributions arise.
First I reiterate Maxwell's very elegant derivation of the single
dimension velocity distribution which turns out to be a gaussian in speed, v. Then the animation shows graphically how the
products of these 1 dimensional speed distributions combine to result in more
interesting higher dimensional distributions.
The animation also converts these speed distributions into energy
distributions in all 4 dimensions.
Maxwell's Derivation of Velocity Distributions
Maxwell claims that the (vx,vy,vz) components are independent of each other so he can write the three dimensional probability function as the product of three one-dimensional probability functions:
![]()
To convert this expression from the case of simple point particles to extended objects with rotational motion, like rotors, we will add another f to the right hand side of the equation:
![]()
where vf=wl where w is the rotation rate of the rotor and l is the distance from its rotation axis to the effective center of
its end masses. We'll assume a symmetric
rotor for the time being.
Now, since the F or fs are not expected to be zero or negative, it is acceptable to take the natural log of both sides of this equation:
![]()
We can take the derivative of this equation with respect to vx:
![]()
Note that the total speed is:
![]()
and therefore we can use the chain rule to express the derivative:
![]()
Now
![]()
so that:
![]()
Then using a previous equation we can write:
![]()
which can be written:
![]()
The next claim is that all of the vx,vy,vz,vf versions of the right hand side of this equation must be equal to the same constant. We will call this constant -b. Then, for vx, we can write:
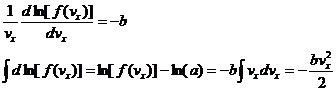
or
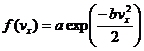
Obviously
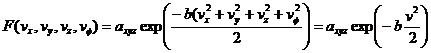
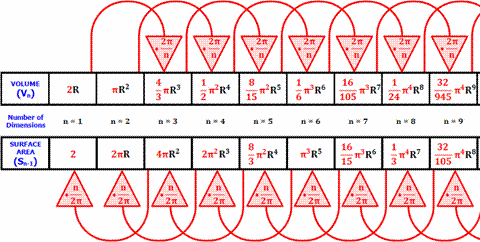
Conversion to Speed Distributions in Various Dimensions
For the speed, v, distribution in two dimensions we must take into account the fact that there are more possible values at large v than at small v. We can think of the product f(vx)f(vy) as a weighted distribution of points in the xy plane. Let
![]()
be the circle centered on (vx,vy)=(0,0) where the square root of the sum of the squares of (vx,vy) is equal to the constant v.
The number of points in the range v to v+dv is then proportional to:
![]()
where
![]()
is just the velocity area increment for a ring of width dv and radius v.
For the speed, v, distribution in three dimensions we must take into account the fact that there are many more possible values at large v than at small v. We can think of the product f(vx)f(vy)f(vz) as a distribution of points in the xyz volume. Let
![]()
be the spherical surface centered on (vx,vy,vz)=(0,0,0) where the square root of the sum of the squares of (vx,vy,vz) is equal to the constant v.
The number of points in the range v to v+dv is then proportional to:
![]()
where
![]()
is just the velocity volume increment for a spherical shell of thickness dv and of radius v.
For the speed distribution in 2 Cartesian coordinates plus rotation we write
![]()
Then
![]()
which is very similar to the case where there are 3 Cartesian coordinates.
For the speed distribution in 3 Cartesian coordinates plus two rotation coordinates we have the expression:
![]()
Then
![]()
Conversion to Energy Distributions in Various Dimensions
The energy is proportional to v2 and the energy increment dE is then proportional to vdv. Then we only need to make the appropriate changes to the speed distributions to convert them to energy distributions.
For 2 dimensions we have the expression
![]()
for the number of points in the energy range E to E+dE. This results in a simple exponential in E.
For 3 dimensions we have the expression
![]()
for the number of points in the energy range E to E+dE.
For 1 dimension, where there is no power of v multiplying the exponential we have
![]()
For 2 Cartesian dimensions plus one rotation dimensions we obtain the same expression as for 3 dimensions.
For 3 Cartesian dimensions plus two rotation dimension, we get the following expression for n(E)
![]()
http://en.wikipedia.org/wiki/Hypersphere