Space Charge and Current Density in a Vacuum Tube

Introduction

This animation shows the charge flow (current density) and charge distribution in a standard electronic vacuum tube like one would see in radios prior to about 1960. In this type of tube, the number of electrons escaping the surface of the heated cathode far exceeds the number of electrons that can reach the positive-voltage anode. The reason this is so is that the cloud of negative electrons between the cathode and anode partially screens the positive potential on the anode reducing the number and average speed of the electrons that actually reach the anode. The math for this space-charge-limited current was first developed by Child and Langmuir.

Figures

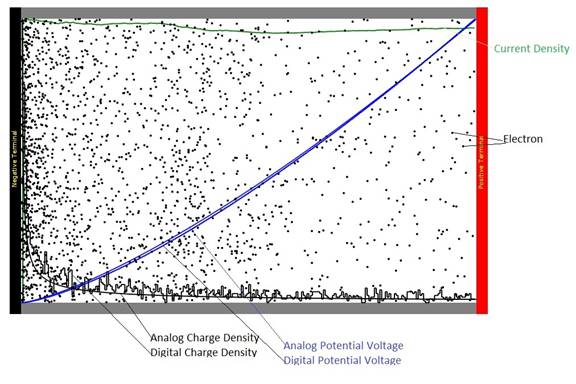
Figure 1: Schematic diagram of the vacuum tube. The space between the negative and positive electrode is exaggerated for clarity of the charge density. Note that the electron charge density is very large (goes to infinity) at the Negative Terminal (black) end of the tube.

Child's Law Derivation with x Dependence

If we let the symbol V be the electric potential, r be the charge density, and e₀ be the permittivity of vacuum we can state the Poisson equation for the potential as:

Since charge is conserved we can also state that:

where J is the spatially constant current density and v is the electron speed which is assumed to be zero at the cathode and to vary according to the electric potential as.

Rewriting the first equation using the definitions of J and v we have:

Let A be defined as:

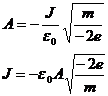
Define

and

so that the equation becomes:

but

Integrating both sides we obtain:

or

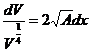
Integrating this equation we have:

Now the anode is placed at x=d where and has positive voltage V=V_e:

solving for A we obtain:

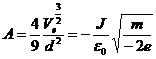
Then solving for J we get:

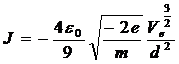
which is Child's law.

We can now solve for the charge density J/v versus x. First note that:

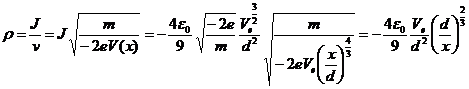
so that r is proportional to x to the -2/3 power and its value at x=0 is infinity while its value at x=d is proportional to V_e.

Adapting The Analog Values to Digital ones

Digitally, the best we can describe the charge density as a large array of bins along the x axis that contain charge corresponding approximately to the (d/x)^(2/3) law given above.

In order to compute the electric field due to this large group of layers of thickness d₁ we use the following summation:

where the layers are centered at positions x_i, separated uniformly by dx, and x_j is an observation coordinate greater than x_i and s(x)=r(x)/d₁ where d₁ is the thickness of each layer.

Similarly to obtain the potential at x_j we use the following summation:

Computing Steady State Current Density from Charge Density Histogram

The current density, J, must be constant spatially:

where n(x) is the number of charges at the histogram column x. Therefore we can write:

Now we must relate the charge speed, v, to n(x). First we need discrete summations for the Electric field potential. If we ignore the electrode potential, V_e, as well as scaling factors for the time being we can use for the E field at the jth bin the summation

Similarly we can use the following summation for the potential at the kth bin:

Where N is the total number of bins. To scale V_k so that it becomes V_e at k=N and 0 at k=0, we use the following normalization procedure. Let

Then to satisfy the conditions at k=0 and k=N we must have:

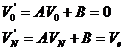
Then A and B are:

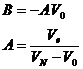
Now we are in position to take the derivative dv/dx with respect to x (or k):

First note that

and that dv/dt is proportional to E which is much simpler than V. Then using the first equation of this section:

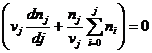
Multiplying through by v_j we get:

The rest of this development will be left to the learner.