Ball in Box Equations

Introduction

`This animation is an attempt to make the ball activity on something like a pool table realistic. To provide this, both ball spin and resonant vibration are included as well as the usual angle of reflection equals the angle of incidence for the ball velocity. I have also included decay rates for velocity, spin, and vibration. The equations below document how this is done.

Equations

Speed and Velocity

As usual, the equations for velocity after bounce from a wall are:

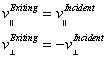(1)

where the parallel subscript refers to the component of the incident velocity parallel to the wall and the perpendicular subscript refers to the velocity component perpendicular to the wall.

Equations 1 indicate that the speed of the ball does not change in bouncing off the wall. The value of the speed is determined by pressing the arrow keys. The decay of speed after keying in a particular speed is determined by the equation:

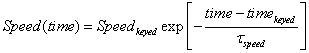(2)

where Speed_keyed is the value of speed that was keyed in with the arrow keys, t_speed is the time constant for speed decay, and time_keyed is the time at which the most recent arrow key press was finished.

Spin

The spin induced by the ball hitting the wall is determined by the following equation

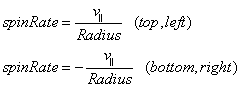(3)

The parallel component of the velocity is defined as positive when it is directed toward more positive x or y and vice-versa. That means that (with positive parallel velocity) spin is counter-clockwise when the ball collides with the top or the left side of the box. Also, the spin is clockwise when the ball collides with the bottom or right side of the box. As you can see here, I have defined counter-clockwise spin as positive. Equation 3 assumes that the ball has no slippage parallel to the wall when it hits and the wall thereby provides all possible spin to the ball. There is a slider named “Spin Transfer Efficiency” whose value (which ranges from 0 to 1) multiplies the right side of Equations 3. The wall also cancels any residual spin that the ball had before it hit the wall. After the ball hits the wall the spin rate decays via the equation

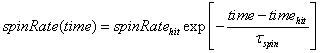(4)

where spinRate_hit is the value of spin that was obtained just after hitting the most recent wall, t_spin is the time constant for spin decay, and time_hit is the time of the most recent wall hit.

Resonance

By resonance I refer to the changes of the ball shape due to hitting the wall. I define the resonant transfer as

where resTransferEff is the value that is provided by its slider. Resonant amplitude also has a decay formula:

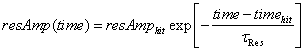
where resAmp_hit is the value of resonant amplitude that was obtained just after hitting the most recent wall, t_res is the time constant for resonance decay, and time_hit is the time of the most recent wall hit.