Accelerated Space Trip Signal
Reception Rates
Introduction
One of the "standard" graphics associated with
accelerated space trips is to show a large group of evenly spaced signals sent
by the inertial frame (earth) to the accelerated frame (rocket) and vice
versa. That might be a worthwhile endeavor
but it would be more interesting to see how the signal reception rates vary as
the space trip continues since this will be some measure of apparent variation
the clock rates. The present document
will compute these reception rates.
Rocket to Earth Reception Rate
To be definite, our signals will be very short light pulses
so we'll use the term pulse from now on.
We'll start with pulses sent from the rocket to earth. These will be sent at equal increments, ,
of rocket proper time so their emission events
will resemble the ticks of the rocket clock.
The displacement at which emission occurs is the rocket displacement, .
To compute for a general acceleration program which has
acceleration phases as well as cruise phases we will need the time integral of
the acceleration
|
|
|
(1.1)
|
where a(t) is the
acceleration as a function of rocket proper time.
Then we can obtain the emission displacement, ,
for the ith pulse, by the following integral
|
|
|
(1.2)
|
The pulses proceed toward the earth at the speed of light
which means that they travel upward in
the Minkowski space time diagram (ct, x)
and toward the earth world line at an angle of 45 degrees. Therefore at t', subsequent to emission, their coordinates will be:
|
|
|
(1.3)
|
We need to compute the time of reception of the ith pulse at
x=0. Obviously,
|
|
|
(1.4)
|
so that we have the difference between reception of the ith
pulse and the (1+1)th pulse
|
|
|
(1.5)
|
We are now ready to compute the retarded rate of reception
for a particular pulse. Note that:
|
|
|
(1.6)
|
and this will cause a difference between reception rate and
emission rate. When tanh is positive
this causes a decreasing rate of reception while when tanh is negative it
causes an increasing rate of reception.
It is the same as a Doppler shift in frequency but its effect is
retarded by the value of x(t)/c.
Then the rate of reception, dn/dt, at time t' is:
|
|
|
(1.7)
|
where dn/dt is the rocket's proper time rate of pulse
emission.
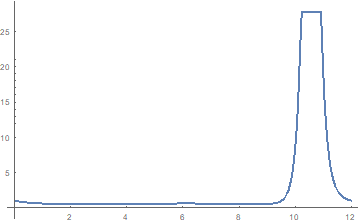
Figure 1: Plot of relative earth reception rate,
dn/dt'/(dn/dt),equation (1.7), as a
function of t for acceleration=1 light year/year2 .
This completes the calculation of the rate of reception from
the rocket to the earth.
Earth to Rocket Reception Rate
The rocket is moving with respect to the world line of the
earth at speed and its distance at time t is
|
|
|
(1.8)
|
The reception rate is Doppler shifted by the following
factor
|
|
|
(1.9)
|
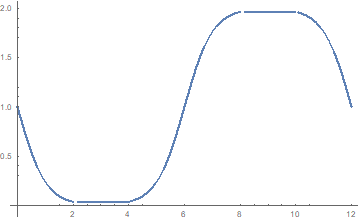
Figure 2: Plot of relative rocket reception rate,
dn/dt'/(dn/dt),equation (1.7), as a
function of rocket proper time, t, for acceleration=1 light year/year2
.

