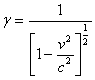Derivation of gamma by experiment
This animation shows how the factor gamma, g, would be determined by experiment. From the point of view of the observer in
system A, system B is moving along the x axis at speed
v. From the point of view of the
observer in system B, system A is moving along the x axis at speed -v.
Therefore it is natural to write:
![]()
where tB and tA
are times measured in the A and B moving systems.
i.e. xA=0 when xB=-vtB and
xB=0 when xA=vtA. In
order to derive g from these equations the following experiment is performed. A light pulse is allowed to propagate
distance xA=c*tA
in system A and a similar light pulse is allowed to
propagate a distance xB=c*tB in system B.
Of course, the speed of propagation has to be c for both observer A and
observer B whether the pulse is observed is in the same system as the observer
or not. Then the equations above become:
![]()
If we multiply the left sides and the
right sides of these equations we obtain a single equation:
![]()
Dividing each side of this equation by tAtB
we obtain:
![]()
From which: