Internal Combustion Engine Particle Animation
Introduction
This animation will show the particle (atom or molecule) kinetics during the stroke of an internal combustion engine. For complete combustion, there must be enough oxygen to completely oxidize the carbon and hydrogen in the fuel. As a simple example, consider natural gas or methane, CH4. It requires two oxygen (O2) molecules to oxidize a single CH4 so the reaction is
|
|
(1.1) |
First note that the total mass and the total number of molecules is the same as before oxidation. That feature remains approximately true for oxidation of gasoline as well. The program assumes that the particle count remains the same during the oxidation process and that the masses of the constituents remain approximately the same.
The mass of CH4 is 16 atomic mass units (amu) and the mass of the O2 is 64 amu and the corresponding number of nitrogen molecules (28 amu each) is 8, the ratio air mass to fuel mass is 18:1. For gasoline the ideal mass ratio is about 15:1. More importantly, the ratio of air particles to methane particles is rather large, 10:1, so I don't try to distinguish between air particles and fuel particles. In this program I model the molecules as hard spheres that usually collide without changing the total energy of the mixture. Of course, when the collisions involve oxidation, the product molecules gain a lot of kinetic energy or heat.
What the program will show is the hysteresis curve of the increase in energy during the compression and ignition process and the corresponding loss of molecular energy during the down-stroke of the piston. The latter loss of energy is what drives the piston and crankshaft through the power cycle.
Combustion Information
The actual process in the combustion combustion chamber of an engine is much more complex than this animation will show. My objective here is to show the gross features of the compression of the charge, its ignition, and how the subsequent expansion is able to provide net energy to the full cycle of the piston.
For a good analysis of the change in the fuel charge temperature (and pressure) under constant volume when CH4 is combusted, see here. The temperature just after combustion is about 2700 degrees Kelvin so, assuming STP for the intake air (300 K), the average molecular energies are increased ten-fold and speeds are increased by a factor of 3.2. This result is very important information for our program and the energy increase factor is a slider variable.
Flame Spreading after Ignition
Although actual flame front speed is a function of fuel charge turbulence due to the intake process, the program shows how the temperature right after the spark is highest in the vicinity of the spark plug in Figure 1.
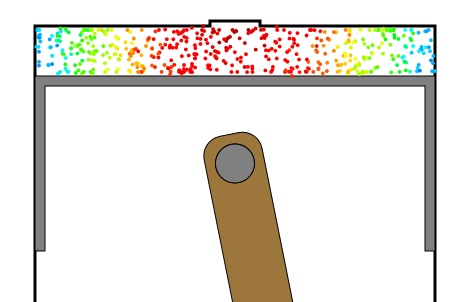
Figure 1: Color-coded diagram of molecule energy spatial variation right after ignition. Red represents the highest energy and blue the lowest. The energy nearest the spark plug is highest since the flame front has not yet spread all the way to the cylinder walls.
The above spatial distribution picture changes very quickly, as shown below, due to particle-particle scattering which "thermalizes" the energies into a Maxwell energy distribution.

Figure 2: Color-coded energies of particles a short time after ignition. Again red is the highest energy and violet is the lowest.
Mechanical Energy per Cycle
Ignition usually occurs about 10% of the stroke before the piston reaches its maximum height in the cylinder (to dead center). After the large (almost instantaneous) increase in energy, the energy is further increased due to the remaining 10% of the compression stroke. As the piston makes its down-stroke, gas kinetic energy is given up to the piston cooling the gas and providing net power to the piston. The equation for the energy given up during a cycle is
|
|
(1.2) |
where the cycle proceeds in the order of time and P is pressure and dV is the volume increment. Since we are modeling only a two dimensional gas, the value of dV is the width of the piston times its depth times the increment in height of the piston. Note that the pressure curve proceeds clockwise in the figure below and therefore dE is a positive number.
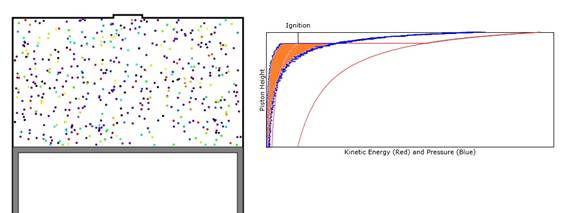
Figure 3: Plot of both pressure (blue) and energy (red) for a full cycle of the piston. Both curves proceed with time in a clockwise direction. The area orange-filled section is proportional to the energy added to the piston in a single cycle.