Animation of Formation of a Depletion Layer at the Junction of Two Semiconductors

Introduction

We will need to animate phonons of a crystal as well as the collisions of electrons with the charge centers of the vibrating nuclei associated with the phonons. These collisions impede the drift in an electric field, as well as the diffusion, of electrons and holes. When the p side of the junction is brought into contact with the n side, holes start to diffuse from the p side into the n side leaving bare negative ions in the p side as well as a net positive charge on the n side. Similarly, electrons start to diffuse from the n side into the p side leaving bare positive ions in the n side as well as a net negative charge on the p side. After sufficient diffusion time, the diffusion is halted due to this buildup of opposite charge density on each side of the junction. This charge density leads to an electric potential distribution (V_{built in}) that opposes the flow of more holes and electrons. When a sufficient electric potential of the appropriate sign is applied across the junction, the potential distribution is overcome and electrons and holes are able to flow again. This latter behavior will also be animated.

Figures:

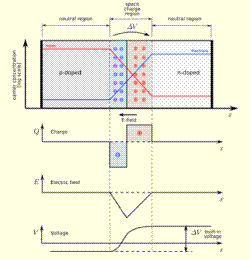
Figure 0:The "standard" model of the charge distribution, electric field E, and voltage V Vs position for a p-n junction.

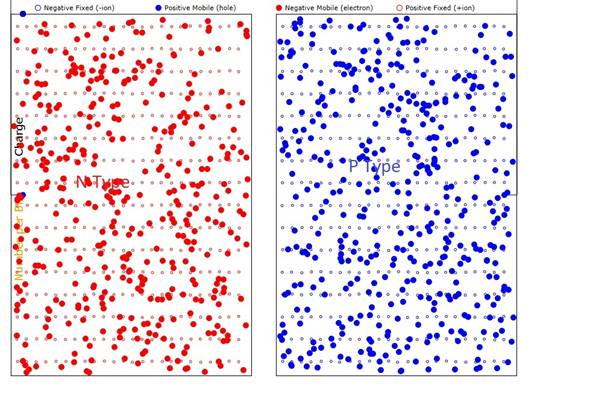
Figure 1. pn junction before fusing All charge types are color-coded. Please read the codes.

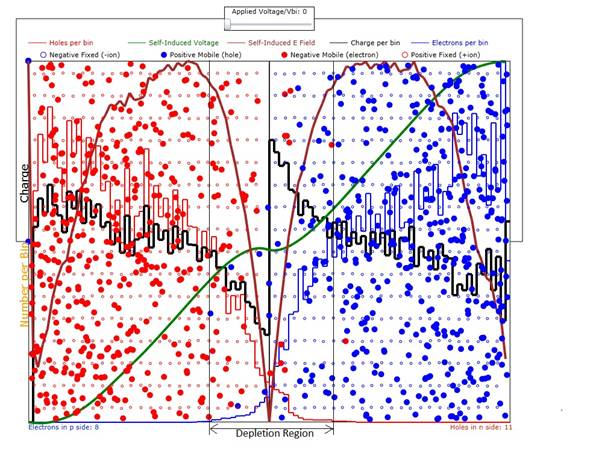
Figure 2. pn junction after fusing. The depletion region is labeled at the bottom of the Figure. All curves and charge types are color-coded. Please read the codes.

Calculations

1. Calculation of the voltage Vs position in the junction area

The voltage is obtained by the Poisson equation in one dimension as:

(1)

where e is the dielectric constant and r(x) is the charge distribution. Note that r does not depend on y and z. If the variation of r is as follows:

(2)

where 2d is the total width of the depletion region and the units of r₁ are coulombs per meter cubed so that the sheet charge density is r₁d for each of the two parts of the depletion layer.

Then the solution for x component of the electric field is while the electric field in the y and z direction is zero.

(3)

We can further integrate E(x) to obtain V(x):

(4)

where V(0)=0 has been chosen.

For a more general sheet-like charge distribution, s (coulombs m^-2), we can suppose a charge of small thickness d₁, centered at -/+ d/2. Let the total charge in the sheet be the same as before

and, to start, center s at x=-/+d/2. The resulting peak E field is the same as for the thick charge

The potentials at -/+ infinity, for the case where the charged layers are centered at -/+ d/2 are the same as before:

To compute the fields for an arbitrary distribution of charge, we can use superpositions of charged layers like s. Note that the peak electric field for s doesn't depend on the spacing of the charged layers but the potentials at -/+infinity are linearly proportional to layer spacing. For example

where the two layers are centered at x=-/+d₂.

In order to compute the electric field due to a large group of layers of thickness d₁ we use the following summation:

where the layers are centered at positions x_i, separated uniformly by dx, and x_j is an observation coordinate greater than x_i.

Similarly to obtain the potential at x_j we use the following summation:

2. Electron/Hole Velocity Response to Potentials

The electron (e) and hole (h) velocities are changed as they traverse the electric potential due to depleted layer. Both e and h have the x component of their velocities reduced when they climb their respective potential energy barriers U_e(x) and U_h(x) where

where e is the elementary charge and is here considered to be positive.

Using Newton's law to compute the velocity change per time increment we have:

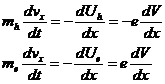
where, t is time and m_h and m_e are the masses of h and e particles, respectively.

Of course, the electron's progress into the p region is with a negative v_x and its v_x is incremented as it climbs its potential hill thereby reducing its rate of progress into the p region. The result of all this is that, in steady state, there are very few h in the n region and very few e in the p region.

3. Electron-Lattice Collisions

While the correct way to handle these collisions is a wavelike treatment using the quantum description of electron wave and phonon waves in the crystal, for simplicity here we will use hard sphere collisions between the electrons/holes (e/h) and the much more massive nuclei at the lattice points of the crystal. That way the thermally excited lattice will impede the diffusion of the e/h particles as is usually expected from electron-phonon collisions.

Since the nuclei are much more massive than the e/h particles, we will assume that no energy or momentum is given up to the nuclei. If the location of the e/h is at (x₁,y₁,z₁) and the nucleus is at (x₂,y₂,z₂), then a unit vector pointing from the e/h to the nucleus is

(5)

where

Thus the only thing that happens to the e/h is to reverse the component of its momentum along the u direction. The new (denoted by prime) velocity vector becomes:

(6)

where, by taking the dot product of u times both sides of the equation, it can easily be shown that

as required.

4. What the Program Calculates

The program computes the position, taking into account the electric field forces and lattice scattering, of all of the mobile carriers (electrons and holes) and sums these in horizontal-axis-correlated (x_i) bins. Since we have a rather low number of carriers per bin, the program sums the number at the ith bin so that what is plotted and used is really the average number of carriers per bin over a long period of time. Since equilibrium is always reached, this averaging does not affect the results. The program then sums the charges (of both mobile and fixed charges) at each of the bins and plots the result. This charge distribution is then used to compute the built-in voltage and electric field distribution as discussed in Section 1 above. The resulting electric field distribution is used, along with the collision dynamics from Section 3, to compute the motion of the charges as discussed above in Section 2.

When a forward bias is applied across the pn junction, the built-in voltage is partially cancelled and the electric field that repels motion of the carriers is reduced so that current can flow. Since the carrier density is lowest at the interface (and therefore the resistivity is highest there) most of the electric field reduction occurs near this interface. When the field at the interface becomes positive, current flows through the pn junction and is depicted by having red electrons flow through the voltage source.

Summary

This has been a demonstration of the power of using simulation of a relatively small number of carriers to get a more heuristic view of some very complicated processes in a simple semiconductor device.