Math for Dragged Roller Coaster Track
Introduction
The idea was to make the roller coaster track as user-interactive as possible. For that reason, period and amplitude of the hills as well as average slope and overall length are adjusted by dragging icons with the mouse. In order to accommodate the radius of the wheels, there are limits to the shortness of the period of the hills.
Description of the track or wheel
trajectory
The equation chosen for the track was the following:
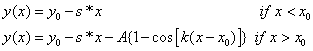 (1)
(1)
where s is the slope, x0 is the horizontal coordinate where the sinusoid starts, and
![]()
is the wave number of the sinusoid with l being the wavelength.
Description of the axle trajectory
Equations 1 give the trajectory or curve of the track where the wheels will roll. But we need to be able to define the trajectory of the axles in order to correctly position the car at all times. Therefore we need another set of equations for this axle trajectory which will have a distance from the wheel curve of precisely the wheel radius a. A straight line that is perpendicular to the wheel curve at point x1 is defined by:
![]() (2)
(2)
where y’(x1) is the derivative (or slope) of y(x)
at x1.
We require that the corresponding point on the axle curve be such that:
![]() (3)
(3)
Equation 3 is easily solved for xa-x1
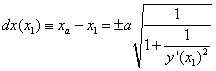 (4)
(4)
Here dx(x1) is the displacement of the axle curve point from the wheel curve point. Also it is important to point out that the sign choice for dx(x) is determined by the sign of y’(x):
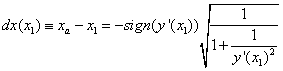
We may now substitute the result of equation 4 into equation 1 and obtain the equation for y coordinate of the axle curve ya(x) :
![]() (5)
(5)
where I have now generalized dx(x1) and y’(x1). This (ya(x)) is the curve that the
axles will follow with the proviso
that the x value for the axle curve
is x+dx(x) i.e. just plot (or define) ya(x) Vs x+dx(x) instead of Vs
x.
Requirements for physical reality
Since the wheel radius, a, is not zero, there are limits on both the amplitude A and the wave number k so that the minimum radius of curvature of the track is more the wheel radius a. The track’s smallest radius of curvature occurs when the first derivative of y is zero. The radius of curvature there is the inverse of the second derivative of y(x) with respect to x:
![]() (6)
(6)
The program automatically limits the size of A to keep rc<a:
![]() (7)
(7)