Tidal Forces due to External Bodies

Introduction

            This will be a very simple treatment of the forces due to gravity on particles, m, on the surface of a sphere of radius r from a large mass, M, that is very far away (distance R) from the first mass.  Since the distance is so great we will not be concerned with the size of mass M but we will need to be concerned with the radius, r, of the small particle of mass m since that surface is where  the particle lies.

Calculations

From the diagram below it is apparent that the distance from M to the particle at the end of the r vector is $\sqrt{{(R-r\cos \varphi )}^2+r^2{\sin }^2\varphi }$   .  Therefore the magnitude of the force on m due to M is

 

$\left|F\right|=\frac{GMm}{R^2+r^2-2rR\cos \varphi }$         (1.1)

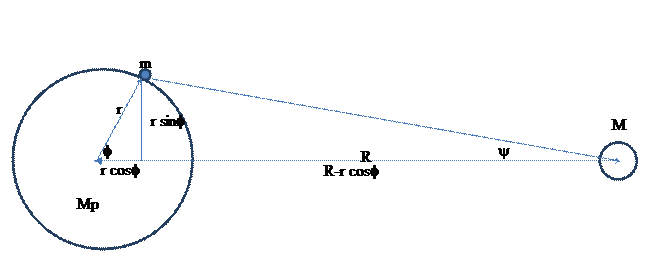
and the vector expression of this force is:

 

$F=\left|F\right|(\cos \psi x-\sin \psi y)$       (1.2)

 

where obviously:

$\psi ={\tan }^{-1}\frac{r\sin \varphi }{(R-rcos\varphi )}$ 

One must realize that the usually larger mass, MP, is also in orbit and in free fall about the common center of mass of M and M_P as shown in Figure 2.

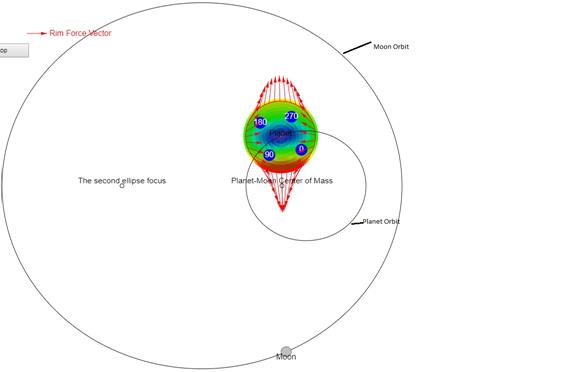
Figure 2:Orbits of planet and moon.

In order to get the net force on the particle, we must subtract the gravity force of the same mass  particle located at the center of the sphere of mass M_P :

$$F_{centered}=\frac{GMm}{R^2}x$$

(1.3)

Therefore the general expression for the net force is:

$$F_{net}=\frac{GMm}{R^2+r^2-2rR\cos \varphi }(\cos \psi x-\sin \psi y)-\frac{GMm}{R^2}x$$

(1.4)

Discussion and Critique

Equation (1.4) as well as the Figure are obviously limited to the plane in which the particle and the centers of both mass M and the sphere of radius r lie.  However this makes a pretty good start in showing the forces on particles over a large section of the sphere of radius r.  Force on circles on the sphere which are above and below the plane of the drawing will generally be smaller as shown by the color plot in Figure 2 where red is the largest force magnitude and blue is the lowest.