Lens Ray Calculation
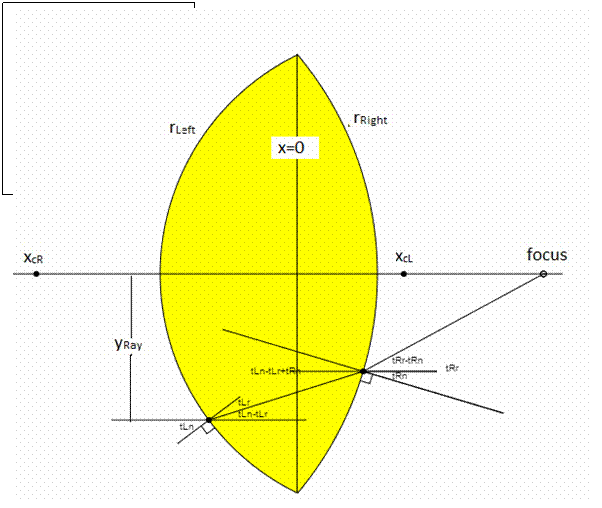
Figure 1: Ray
trace showing the incident ray, the refracted rays at both surfaces, as well as
the normals to the surfaces where the rays are refracted. The angles that are needed for the refraction
calculations are labeled as described below.
In the labels, the first letter t means that it is referring
to an angle as in the greek letter theta.
The second letter, L or R, refers to the Left or Right
surface.
The third letter can be either r or n. r refers to a refracted angle with respect to
the surface normal and n refers to the angle of the surface normal with respect
to the x axis. This labeling is needed
in order to easily see what are the incident angles and the refracted angles
and the final ray angle with respect to the x axis.
Calculations
A double convex lens that is centered on the x axis is defined
by the left and right radii of curvature, rL and rR. For convenience we will define the signs of
these curvatures so that the xL(y)<0 and xR(y) >0. If the radius of the lens is rLens
then the centers of these curves are at:
|
|
|
(1.1)
|
The x location of any point y<rLens on the
lens is:
|
|
|
(1.2)
|
Note that when y=rLens, x=0 as expected for these
definitions. Also note that when
y<>0, xL is less than zero while xR is greater than zero.
If an incident ray that is parallel to the x axis hits the
left surface is at then its corresponding x coordinate is at
|
|
|
(1.3)
|
Also the angle between the surface normal at yLi
and the ray is
|
|
|
(1.4)
|
Let the index of refraction of the lens be n.
Snell's refraction law is:
|
|
|
(1.5)
|
where is the angle between the surface normal and
the refracted ray.
Then, using equations (1.4)
and (1.5),
the angle between the normal and the refracted ray is
|
|
|
(1.6)
|
The angle of the refracted ray with respect to the x axis is
|
|
|
(1.7)
|
which is a negative angle when y>0 and positive when
y<0 so that the refracted ray slopes toward the x axis.
The slope of he refracted ray is then
|
|
|
(1.8)
|
The y coordinate of the refracted ray in the lens can be
written as:
|
|
|
(1.9)
|
In order to compute the intercept of yr with the
right hand surface of the lens we can re-write equation (1.9)
using equation (1.2)
and obtain
|
|
|
(1.10)
|
where yRr is the y intercept of yr(x)
with the right surface of the lens and it to be solved for.
We can greatly simplify solving equation (1.10)
by separating out the constants by letting
|
|
|
(1.11)
|
and then equation (1.10)
becomes:
|
|
|
(1.12)
|
We may conveniently square both side of equation (1.12)
and solve for yRr and obtain:
|
|
|
(1.13)
|
Having obtained the y intercept using the + sign before the
radical, we can use equation (1.2) to obtain the x
intercept:
|
|
|
(1.14)
|
Finally we may use Snell's law for the refraction of the ray
as it exits the right hand surface. The refracted ray's incidence angle with
respect to that normal is:
|
|
|
(1.15)
|
Since
|
|
|
(1.16)
|
we have the refracted angle:
|
|
|
(1.17)
|
With respect to the x axis this angle is:
|
|
|
(1.18)
|
Finally the slope of the this ray is:
|
|
|
(1.19)
|
The y coordinate of the exiting ray can be expressed by:
|
|
|
(1.20)
|
Solving equation (1.20)
for x at yexit=0, the ray will intercept the x axis at location:
|
|
|
(1.21)
|
|
|
|
|
