Quantum Modes of Particle in a 1D Square Potential Well of Finite Depth

The modes are the eigenvalues and eigenvectors (psi(x))of the second order Schrodinger equation (SE)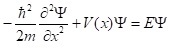 , where h with the bar (hbar) is the Planck constant, m is the mass and E is the energy of the particular mode whose wave function is the eigenvector. For this program I have chosen to set the Planck constant (divided by 2*pi), hbar, equal to 1 Joule second and the mass, m, equal to 1 kilogram. Although the SE can also express the time dependence of the wave function, only the steady state eigenmodes will be computed here. Of course the potential in quantum field theory is 3 dimensional but three dimensions are hard to depict so I have chosen 1 dimension, x, here. The black trace is the potential that the particle is in,. The eigenvalues of the particular setup are depicted with small black circles at each eigenvalue. By placing the mouse on one of these circles and clicking, the eigenvector (spatial mode) of that eigenvalue will be drawn as a green trace. From the Schrodinger Equation solutions we obtain three important types of information about how a particle moves in the potential V(x).
1. The energies, Ei, which are the eigenvalues of the stationary state modes.
2. The square of the amplitudes of the eigenvectors, vi, which is the probability density for the position, x, of the particle.
3. The spatial frequencies, k(x) Vs position x of the eigenvectors to which the particle momentum is proportional.
k(x) is constant and real inside the potential well but imaginary outside its bounds. Since k is constant, that would indicate that the speed of a particle that it represents would also be constant.