Curator Welcome
Time Dependent Wave Equation 1D One Dimensional Optical Resonator Modes
Gas Physics Introduction
Gas Physics Introduction Chapter 1:Energy Distribution Evolution Energy Diffusion from Mono-energetic of a Three Dimensional Gas Rotating Gas in a 3D Toroid Gas Velocity Equilibration 2D Gas Velocity Equilibration 3D Circulating Gas in a Wind Tunnel Density Modulated Rotating Gas in a 3D Toroid Position Diffusion (Mixing) of a Three Dimensional Gas Energy Distribution 3D with MathJax Equations and Embedded Canvases Gas Energy Distributions 2D Rigid Rotors Energy Distribution 2D 1D Gas Energy and Momentum Distribution Rotor Energies 2D Rotor Energies 3D H2O Energies 3D CO2 Energies 3D 2D Rigid Arrays with Rotation and Translation 3D Rigid Arrays with Rotation and Translation Gas Energy Distributions 1D, 2D, 3D Chapter 2:Particle Scattering Effects
Inelastic Collision Conversion to Internal Energy Brownian Motion Animation 2D Using Hard Sphere Scattering Large Disc Kinetics 2D Condensation of a Gas on a 2D Solid Maxwell's Demon Energy Seperator 2D Minimize Final Energy 2D and 3D Gas Diffusion 2D Gas Expansion 2D Linear Gas Expansion 2D Constant Pressure Gas Expansion 2D Circular Gas Explosion 2D Circular MagnetoCaloric Effect 2D Convection Loops in a Numerical Gas Chapter 3: Gas Energy Equipartition Energy Equipartition of a Two Dimensional Gas with Two Different Masses Energy Equipartition of a Three Dimensional Gas with Two Different Masses Gas Energy Equipartition 3D
Chapter 2.1
Chapter 2.2
Chapter 2.3
Chapter 3.1
Chapter 3.2
Chapter 3.3
Chapter 4.1
Chapter 4.2
Chapter 4.3
Photoelectric Effect Alpha Particle Emission from a Large Nucleus 2D Black Body Emission from Charged Harmonic Oscillators Quantum Animation of Energy Band Gap 1D Animation of Quantum Wave Packets in a pn Junction 1D Quantum Mirror Focusing by Iterating the Schrodinger Equation Quantum Lens Focusing by Iterating the Schrodinger Equation Quantum Two Mirror Resonator by Iterating the Schrodinger Equation Entangled Quantum Object Propagation in a Parabolic Potential Classic and Quantum Object Propagation in a Parabolic Potential Accurate Wave Packet Propagation in a Parabolic Potential Comparison of Quantum to Classical Physics 1D-Time Dependent Accurate Wave Packet Propagation in a Swaged Potential Series Solution of Wave Packet Propagation in a Infinite Square Potential Propagation of a Wave Packet in a Parabolic Potential Propagation of a 2D Wave Packet in a 2D Parabolic Potential Propagation of an Asymmetric Shaped Wave Packet in a 2D Parabolic Potential Two Slit Diffraction by Iterating the Schrodinger Equation Two Potential Slit Diffraction by Iterating the Schrodinger Equation Propagation of an Electron Wave Packet in an Infinite Square Well (Series Solution) Propagation of a Free Wave Packet (Series Solution) Series and Algebraic Solutions for Propagation of a Wave Packet in a Parabolic Potential Comparison of Quantum to Classical Physics 1D-Time Independent Mexican Hat Stationary Quantum States of a Finite Square Potential Well Various Wave Packet Motion in a Finite Square Potential Well Various Wave Packet Motion in a Swaged Potential Well Comparison of Quantum to Classical Physics 1D-Time Independent Cosine/Parabola Electromagnetic Modes of a 2D Cavity Black Body Radiation Experiment and Theory Emission of the Inner Walls of a Black Body Cavity Multiple Slit Diffraction Statistics of Indistinguishable Dice or Particles Quantum Field Collapse Visualization Matrix Operations and Eigenmodes
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Tumbling Block on Inclined Plane New Roller on Inclined Plane Sliding Block on Inclined Plane Classic Objects Motion 1D Generation of Curve for Fastest Time between Two Points Curve for Fastest Time between Two Points Bead Sliding On a Stiff Wire Sound Wave in Two Solid Media Mechanical Properties of a 2D Numerically Modeled Lattice Vibrating Reed Numerical Model 2D Laminar Flow of a Fluid in a 2D Bearing Animation of a Fountain 2D Gravity Leveling of a 2D Liquid Longitudinal and Shear Wave Sound Speed in a 2D Lattice Mechanical Properties of a 2D Numerically Modeled Lattice Vibration Frequencies of a 2D Numerically Modeled Lattice Damped Harmonic Oscillator Motion and Modes of a Particle in a Mexican Hat Potential Forced Oscillator Roller Bearing Cam and Roller Follower Simple Hybrid Gear Train Ratchet Animation Child's Swing Height Increase Mechanics Roller Chain Animation Elasticity of 3D Gas Driving a Piston Free to Forced Harmonic Oscillator Transition Physics of Mounting a Tire on a Rim Physics of a Pendulum Clock Escapement Physics of a Gas Pressure Gauge
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Physics of a Gas Pressure Gauge Ion Drift in Neutral Particle Sea Diffusion Equation Solved by Finite Difference Method Linear Particle Diffusion Heat Flow 1D with Time Dependent Boundary Solid Cube in Liquid Column Drag on a Large Sphere Due to a Digital Gas Animation of a Gas Centrifuge Laminar Flow of a Gas in an Annular Space Laminar Flow of a Fluid in a 2D Bearing Incompressible Fluid Flow through a Constriction Fluid Flow Due To Pressure Gradients
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Parallel Resistors Gas Discharge Animation Oscilloscope Animation Permanent Magnet in Solenoid Cross Product of Two Vectors Magnetic Braking with Cylindrical Geometry Stopping a Falling Magnet by Eddy Currents Magnetic Brake Magnetic Field of a Long Solenoid Coil Light Propagation in a Transparent Dielectric Material Dipole Array Animations Angular Distribution of Emission of Arrays of Excited Dipoles Geometric Derivation of Snell's Refraction Angle Law Electromagnetic (EM) Wave Response to a Row of Dipoles Electromagnetic (EM) Wave Response to a Single Dipole Optics of a Transparent Plate by Iterating the Maxwell Wave Equation Diffraction by Iterating the Maxwell or Schrodinger Wave Equations Lens Focusing by Iterating the Maxwell or Schrodinger Wave Equations Optical Wave Packet Propagation by Finite Difference Matrix 1D Potential(x,y) Using Laplace's Equation Div(gradV)=0 with Variable Boundary Geometry Potential(x,y) Using Laplace's Equation Div(epsilon*gradV)=0 Laplace's Equation Div(gradV)=0 with Mixed BCs Potential(x,y) for Surface Electrodes with Dielectric Slab Dipolar Media Field Plots LCR Oscillator Animation Beam Trajectory of a Moving Laser Beam Trajectory in a Square Ring Laser Doppler Effect Converting Magnetic Forces to Electric Forces Converting Permanent Magnet Orbital Moments to Solenoid Currents Electron Beam Collimation by Axial Magnetic Field Electron Buncher for Klystron Charged Particle Spatial and Speed Bunching Electrical Conduction-Particle Picture Electromagnetic Bell Triode Vacuum Tube
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
E=mc^2 and Mexican Jumping Bean Radar Pulse Return Time Interval Experiment to Determine Gamma Current Loop with a Rotating Test Particle Moving Fabry-Perot Interferometer Space Time Invariant Intervals of a Moving Clock Relativity Transformations by Requiring Simulataneity Accelerated Space Trip Clock Times and Rates Minguzzi Invariant Inertial Frame Time Accelerated Space Trip with Light Pulse Signaling
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Solar Power Generation Planet Formation Illumination of Planets Change of Orbit due to Asteroid Impact Earth Time Zones Day Lengths Astronomical Aberration Kepler Planetary and Sun Orbits Model of Ocean Tides Gravity Course Iteration Spacecraft Speed Assistance by Gravity Hohmann Transfer from One Circcular Orbit to Another Star Distances Using the Parallax Method
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Semiconductor Electron Energies and Band Gap 1D Semiconductor Electron Energies and Band Gap 2D Simple Fermi Surface p-nJunctionDiode Depletion Width Temperature Dependence of 2D Fermi-Dirac Particles
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Assembly of 3D Parts Using Javascript Web Graphics Library 3D Compared to Javascript 3D Graphics 3D Graphics Tutorial Beginnings Proof of Pythagoras a^2+b^2=c^2
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Multiple Slider Animation Template for Plotting with HTML Enhanced Sliders or Ranges Collapsible Dropdown Menu Example Arrow Functions Fast Fourier Transform (FFT) Demonstration
Animation of a Progress Bar
Template for Scientific Plots
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Time Dependent Wave Equation 1D One Dimensional Optical Resonator Modes
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Probability of Birthday Match Random Creation of Probability Function Profiles Two Dies Probability Distribution Three Dies Probability Distribution
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Light Rays in a Transparent Isosceles Prism Light Ray in a Series of Wedges of Various Index of Refraction Snells Law of Refraction Refraction Due to Dipoles in Two Media Refraction and Reflection Two Media Animation of Concave Mirror Reflection Animation of Convex Lens Refraction Prism Refraction-Wave Picture Thick Lens Ray Trace Monochromator (Czerny-Turner Type) Wavelets from Concave Mirror> Thick Lens Focusing
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Sagnac Effect Fiber Optical Gyro (FOG) Ring Laser Gyro (RLG)
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Paticle Motion in a Venturi: Wall Reflections Paticle Motion in a Venturi Potential Elliptical Ion Trap Using Boundary Potential Distribution Prediction of Hard Disc Collision Time and Position Rigid Rotor Collisions
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Acoustic Wave with Built-in Pressure Acoustic Waves in 2D Numerically Modeled Solid Wave 1D on a Linear Array Waves on Discrete Model of Vibrating String Linear Acoustic Wave in a 3D Gas Spherical Acoustic Wave in a 3D Gas Laterally Perturbed Two Dimensional Gas with Lennard Jones Repelling Forces Longitudinally Perturbed Two Dimensional Gas with Lennard Jones Repelling Forces
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Bicep and Forearm Animation Blood Pressure Measurement Multiple Dose Residual Medicine Vs Time The Eye and its Resolution Breathing Animation Scoliosis Animation Muscle Animation
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Scattering from a Crystalline Target 2D Scattering from a Crystalline Target 3D
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Energy Conduction in a 2D Numerically Modeled Solid Lattice Unbalanced Gas Dynamics:Energy Flow in a Gas
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12

Hover over the menu bar to pick a physics animation.

Black Body Emission from a Hot Vibrating Solid

The goal of this is to examine what kind of particle movement distributions could result in Planck's black body frequency distribution equation:

`(d^3P)/(dAdOmegadf)=(2 f^2)/c^2 (hf)/(e^((hf)/(k_BT_K))-1) (1)`

where `(d^3P)/(dAdOmegadf)` is the power per unit area emitted into a 1 Hz band width and into unit solid angle. Here f is the frequency, c is the speed of light in vacuuum, `T_K` is the absolute temperature, `k_B` is Boltzmann's constant and h is Planck's constant. At first glance it looks as if `(d^3P)/(dAdOmegadf)` goes to infinity for `(hf)/( k_BT_K)->0` and finite temperature, but if we expand the exponential in the denominator for `(hf)/( k_BT_K) "<<"1` we see that `(d^3P)/(dAdOmegadf)` becomes

`(d^3P)/(dAdOmegadf)((hf)/( k_BT_K) "<<"1)=(2 f^2)/c^2 k_BT_K (2)`

It is important to define what we mean by a black body: It is a surface that absorbs all radiant energy falling on it. The term 'black' arises because incident visible light will be absorbed rather than reflected, and therefore the surface will appear black. However, for an isolated system, the energy will generally be re-emitted at longer wavelengths. The temperature `T_K` can be achieved by radiation at any wavelength. Or it can be achieved by heating with a resistive heater and the resulting emission spectrum will not change. A black body may be either a flat black surface or a cavity with a very small hole in it to permit observation of the radiation spectrum. For the present simulation we will assume a black surface that contains many quantum harmonic oscillators. Max Planck's early papers on his radiation law assumed many different non-interacting oscillators whose frequencies spanned the black body radiation spectrum. Later he had to accept that any oscillators had to interact with oscillators of different frequency. Otherwise, if the black body was heated by applying radiation at only one frequency, how would the oscillators at all the necessary frequencies of the black body frequency distribution re-radiate? Actually we could assume damped harmonic oscillators since we know that they will eventually lose their energy to heat. Take the example of the quartz crystal oscillator in your wrist watch 1. Its Q factor is about 25,000 which means that it oscillates about `25000/(2pi)` cycles before its kinetic energy is reduced to 1/2 of its original value. This energy will heat its surroundings just as radiant energy heats a surface around where it is absorbed. For damped (interacting) quantum oscillators the math gets very cumbersome 2 so here we will just animate classic harmonic oscillators.

Canvas 0: Planck Black Body Frequency Distribution
`k_BT value: 0.005
If the surface is isolated and in a vacuum, then, at constant temperature, the total radiant energy emission will equal the total radiant energy absorption. We don't have to apply what we usually think of as radiation to the surface. We can instead apply resistive heaters to the surface to achieve the temperatures needed for equations 1 and 2. When incident radiation is at a frequency higher than the mean frequency, then the surface must have processes that generally degrade the photon frequency so that it can follow the radiation curve given in equation 1. These processes are always going to involve charge accelerations and thereby charge position changes. It is these charge motions that I wish to animate here.
Spreadsheet 0: Frequency of a Charge Displaced
3 Angstroms

Defining the Emission Entities

To do that, we first need to know the classic power output of a single charge (or dipole) vibrating at frequency f. The vibrating charge will be called a dipole and its carrier can have the mass of just an electron or it can have the effective mass of one atom of a polar molecule. An example of a polar molecule is carbon monoxide (CO) which has a dipole moment of `0.122 D` (Debye where a Debye is 0.0208 electron nm) for which CO dipole moment works out to 0.0025 electron nm. Then we need to choose a surface number distribution of these charges that can result in the power per unit frequency bandwidth given in equation 1. The power per unit solid angle averaged over `4pi` steradians at frequency f and with a dipole moment `p_0` is the following expression:

`(dP)/(dOmega)=pi^2 p_0^2 /(3 epsilon_0) f^4/c^3(3)`

where `p_0` is:

` p_0=e d`

where `e` is an electron charge and `d` is the amplitude of its motion.

Dimensional Analysis of Equation 3

Note that `f/c=1/lambda` so that equation 4 becomes

`(dP)/(dOmega)=pi^2 f p_0^2 /(3 epsilon_0 lambda^3)(3a)`

We know that a term like

`(Qq)/(4 pi epsilon_0 r)`

is the potential energy of charge q at distance r from charge Q. Then equation 3a has the same dimension except the potential energy is multiplied by frequency f and becomes energy per unit time and is power which is what wanted to prove.

The power per unit frequency (per Hertz bandwidth) is then:

`(d^2P)/(d Omega df)=4/(3epsilon_0) pi^2 p_0^2 (f^3)/c^3 (4)`

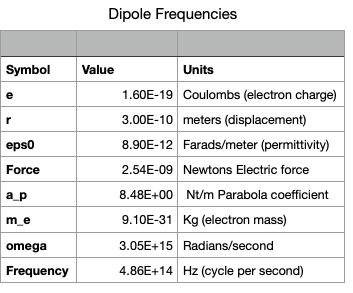
Canvas 1: Classic Harmonic Oscillator Dipoles
We have assumed that the dipoles that contribute to the power have random orientation and therefore their power is distributed over `4pi` steradians. Electric quadrupoles and magnetic dipoles also exist but we will consider only electron dipole moments here.

Next we should consider what the dipole frequency might be. The typical dipole electron bound to a much more massive nucleus of the same but oppositely signed effective charge has an amplitude of order `d=3cdot10^-10` meters which results in a force of (see Spreadsheet 0)

`F= e^2/(4 pi epsilon_0 d^2)=2.5 cdot 10^-9 " Newtons"`

For this animation, since I want to adjust frequency easily, I will model the electron potential, V, as that of a harmonic oscillator. The harmonic oscillator also has the advantage that the temperature dependence of its energy distribution is the same as that in the Planck black body emission equation. In fact the energy distribution of an assembly, N, of harmonic oscillators is

`U(f,T)=Nhf(1/2+1/(exp((hf)/(k_BT_K))-1))`

Our definition of the harmonic oscillator potential is:

`V=a_p/2 d^2`

so the force is:

`F=-a_p d`

The force just computed implies a harmonic oscillator potential coefficient of

` a_p=(2.5 cdot 10^-9)/(3 cdot 10^-10)=8.5` Newtons per meter.

Then the radian frequency is

`omega=sqrt(a_p/m_e)=sqrt((8.5)/(9.1 cdot 10^-31))=3 cdot 10^15`
and the cycles per second are: `f=omega/(2 pi)=4.9 cdot 10^14 Hz`

where `m_e` is either (here) the electron mass or that of the polar atom that carries the charge. This is just a typical frequency for visible light.

Defining the Absolute Temperature (Boltzmann Factor)

We have seen that the factor `k_BT_K` always corresponds to the average kinetic energy, `KE` of the particles of the system. The average kinetic energy is a sum over all `KE_i` of the system:

`KE_("average")=1/n sum_1^n(KE)_i`

In the present simulation, the only significant kinetic energy is that of the vibrating electrons or polar atom. Therefore one requirement of the numerical matching of the Planck black body equation (1) is that the denominator of the equation read:

`k_BT=1/n sum_(i=1)^(i=n)(KE)_i`

where n is the total number of dipoles
Then the denominator of the Planck equation becomes:

`e^((hf)/(k_BT))-1=e^((hf)/(1/n sum_1^n(KE)_i))-1`

But what is the form of `KE_i`? It is related to the oscillator frequency and displacement in a simple way. The maximum value of KE is the same as the peak value of the potential energy.

`KE_(max)=1/2 a d^2=1/2 m_e omega^2 d^2=2 pi^2 m_ef^2 d^2`

and, of course, the time average kinetic energy is 1/2 of `KE_(max)`. Then the denominator in the both the Planck equation and dipole energy power equation becomes:

`e^((hf)/(k_BT))-1=e^((hf)/ (pi^2 m_e/n sum_1^n(f_id_i)^2))-1`

Matching the Frequency Distribution of the Planck Equation

To match the frequency distribution we have to choose a dipole areal density and power distribution `n(f_i)P_i` that agrees with equation 1. So we have the following equation:

` (dn)/(dA)(d2P)/(dfdOmega)=(4pi^2)/(3epsilon_0) p_0^2 (f^3)/c^3=`
`(2 f^2)/c^2 (hf)/(e^((hf)/(k_BT))-1) (6)`

The energy distribution of harmonic oscillators is:

`(dE)/(dhf)=(1/2+1/(exp((hf)/(k_BT))-1))`

and we can ignore the `1/2` since that is the zero point energy and can't participate in emission. Then equation 6 becomes:

` (dn)/(dA)(d2P)/(dfdOmega)= (dn)/(dA) hf(1/(exp((hf)/(k_BT))-1))(4pi^2)/(3epsilon_0) (f^2)/c^3 p_0^2=`
`(2 f^2)/c^2 (hf)/(e^((hf)/(k_BT))-1) (6)`

Now we must insert the value `p_0=ed`. Then

` (dn)/(dA) (1/(exp((hf)/(k_BT))-1))(4pi^2)/(3epsilon_0) (ed)^2 f^3/c^3= (2 f^2)/c^2 (hf)/(e^((hf)/(k_BT))-1) (6a)`

We have some options of choice of parameters to cause this equation to be valid. We can choose the distributions of the dipole lengths `d` and we can choose dn/dA. The dipole lengths `d` change the kinetic energy distribution which is the same as changing the effective temperature. So we are left with computing `(dn)/(dA)` to satisfy equation 6a.

` (dn)/(dA)= h(epsilon_0)/(4pi^2 (ed)^2 f/c) (7)`

Dimensional Analysis of Equation 7 Let the character `l` denote a length and the character `U` denote an energy. Note that the denominator has units `le^2` while the numerator has units ` epsilon_0U`. We already saw for equation 3 that the ratio `e^2/epsilon_0` has units `Ul` so that `epsilon_0/e^2` has units of 1/(Ul). Therefore the ratio of numerator to denominator has units of 1/length^2 as expected.

Dipole Motion Amplitude

The treatment above does not specify what must be the dipole motion amplitude, `d`. Using the areal density to match a widely varying frequency distribution is difficult because it requires too many dipoles at frequencies where the black body irradiance is very large. Therefore we will instead satisfy equation 6a with a constant `(dn)/(dA)`and vary the amplitude `d` of the dipoles. Looking at equation 7 it is obvious that `(dn)/(dA)` can be constant if `d^2f/c=d^2/(lambda)` is constant. So the new strategy is to choose a reasonable `(dn)/(dA)` and then choose a `lambda_0` and `d_0` that enable equation 7 to match the Planck energy distribution. Then we have:

`d^2=d_0^2lambda/(lambda_0)=d_0^2(f_0/f) (8)`

so we just need to choose fairly small total area and satisfy equation 8 at random sites.

Defining the Dipole Orientation and Motion

We have two physics requirements:

1. The center of mass of the dipole must not move during its oscillation cycle

2. The net charge of he dipole must be zero

The first requirement results in the oscillation displacement of the end masses being inversely proportional to their masses and opposite in direction with respect to their center of mass. The second requirement just means that the dipole molecule is not ionized. A third aspect is that the dipole orientation is random since there is no reason to assume the entire surface is a crystal. Assume that the orientation of a given dipole is `phi` and the static separation is `d_0` and the end masses are `m_1` and `m_2`. Then the static position of its charges with respect to its center of mass (CM) is

`x_1=m_2/(m_1+m_2)d_0 cos phi`
`y_1=m_2/(m_1+m_2)d_0 sin phi`
`x_2=-m_1/(m_1+m_2)d_0 cos phi`
`y_2=-m_1/(m_1+m_2)d_0 sin phi`

Let the amplitude of the change in separation of the dipole ends be denoted `a` and the oscillation phase is `theta=2 pi ft` so that the maximum change in separation becomes `2a` Then the end charge positions become

`x_1=m_2/(m_1+m_2)(d_0+a cos theta) cos phi`
`y_1=m_2/(m_1+m_2)(d_0+a sin theta) sin phi`
`x_2=-m_1/(m_1+m_2)(d_0+a cos theta)cos phi`
`y_2=-m_1/(m_1+m_2)(d_0+a sin theta) sin phi`

Since the charges at the ends are equal and opposite, the dipole moment `bb p` is:

`bb p=-2e(m_2-m_1)/(m_2+m_1)a cos theta bb hat d_0`

where bold letters denote vectors and `bb hat d_0` is a unit vector in the direction of the vector `bb d_0`. Then, if `m_2 ">" m_1` and the charge on `m_2` is `+e` as one might expect, and `a cos theta>0`, the direction of the dipole moment is opposite that of `bb hat d_0`. A group of animated dipoles is shown on Canvas 1.

Description of the Animations

Dipole photon emission occurs randomly and its energy Vs frequency spectrum follows the Planck spectrun in equation 1. Canvas 0 shows the accumulation of photon energies in bins that finally match the Planck spectrum Also shown are the colored fill and smooth plot there. In order to show random filling of the bins, a special mapping onto integers of the frequency spectrum curve was done using the function mapKs().

The same mapping was done to randomly specify the frequencies of the animated dipoles in Canvas 1. The amplitudes of vibration of the dipoles was according to equation 8. Canvas also 1 shows random emissions in the form of lightning bolts and their color corresponds to the wavelength associated with the frequency of oscillation of the dipoles.