Curator Welcome
Time Dependent Wave Equation 1D One Dimensional Optical Resonator Modes
Gas Physics Introduction
Gas Physics Introduction Chapter 1:Energy Distribution Evolution Energy Diffusion from Mono-energetic of a Three Dimensional Gas Rotating Gas in a 3D Toroid Gas Velocity Equilibration 2D Gas Velocity Equilibration 3D Circulating Gas in a Wind Tunnel Density Modulated Rotating Gas in a 3D Toroid Position Diffusion (Mixing) of a Three Dimensional Gas Energy Distribution 3D with MathJax Equations and Embedded Canvases Gas Energy Distributions 2D Rigid Rotors Energy Distribution 2D 1D Gas Energy and Momentum Distribution Rotor Energies 2D Rotor Energies 3D H2O Energies 3D CO2 Energies 3D 2D Rigid Arrays with Rotation and Translation 3D Rigid Arrays with Rotation and Translation Gas Energy Distributions 1D, 2D, 3D Chapter 2:Particle Scattering Effects
Inelastic Collision Conversion to Internal Energy Brownian Motion Animation 2D Using Hard Sphere Scattering Large Disc Kinetics 2D Condensation of a Gas on a 2D Solid Maxwell's Demon Energy Seperator 2D Minimize Final Energy 2D and 3D Gas Diffusion 2D Gas Expansion 2D Linear Gas Expansion 2D Constant Pressure Gas Expansion 2D Circular Gas Explosion 2D Circular MagnetoCaloric Effect 2D Convection Loops in a Numerical Gas Chapter 3: Gas Energy Equipartition Energy Equipartition of a Two Dimensional Gas with Two Different Masses Energy Equipartition of a Three Dimensional Gas with Two Different Masses Gas Energy Equipartition 3D
Chapter 2.1
Chapter 2.2
Chapter 2.3
Chapter 3.1
Chapter 3.2
Chapter 3.3
Chapter 4.1
Chapter 4.2
Chapter 4.3
Photoelectric Effect Alpha Particle Emission from a Large Nucleus 2D Black Body Emission from Charged Harmonic Oscillators Quantum Animation of Energy Band Gap 1D Animation of Quantum Wave Packets in a pn Junction 1D Quantum Mirror Focusing by Iterating the Schrodinger Equation Quantum Lens Focusing by Iterating the Schrodinger Equation Quantum Two Mirror Resonator by Iterating the Schrodinger Equation Entangled Quantum Object Propagation in a Parabolic Potential Classic and Quantum Object Propagation in a Parabolic Potential Accurate Wave Packet Propagation in a Parabolic Potential Comparison of Quantum to Classical Physics 1D-Time Dependent Accurate Wave Packet Propagation in a Swaged Potential Series Solution of Wave Packet Propagation in a Infinite Square Potential Propagation of a Wave Packet in a Parabolic Potential Propagation of a 2D Wave Packet in a 2D Parabolic Potential Propagation of an Asymmetric Shaped Wave Packet in a 2D Parabolic Potential Two Slit Diffraction by Iterating the Schrodinger Equation Two Potential Slit Diffraction by Iterating the Schrodinger Equation Propagation of an Electron Wave Packet in an Infinite Square Well (Series Solution) Propagation of a Free Wave Packet (Series Solution) Series and Algebraic Solutions for Propagation of a Wave Packet in a Parabolic Potential Comparison of Quantum to Classical Physics 1D-Time Independent Mexican Hat Stationary Quantum States of a Finite Square Potential Well Various Wave Packet Motion in a Finite Square Potential Well Various Wave Packet Motion in a Swaged Potential Well Comparison of Quantum to Classical Physics 1D-Time Independent Cosine/Parabola Electromagnetic Modes of a 2D Cavity Black Body Radiation Experiment and Theory Emission of the Inner Walls of a Black Body Cavity Multiple Slit Diffraction Statistics of Indistinguishable Dice or Particles Quantum Field Collapse Visualization Matrix Operations and Eigenmodes
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Tumbling Block on Inclined Plane New Roller on Inclined Plane Sliding Block on Inclined Plane Classic Objects Motion 1D Generation of Curve for Fastest Time between Two Points Curve for Fastest Time between Two Points Bead Sliding On a Stiff Wire Sound Wave in Two Solid Media Mechanical Properties of a 2D Numerically Modeled Lattice Vibrating Reed Numerical Model 2D Laminar Flow of a Fluid in a 2D Bearing Animation of a Fountain 2D Gravity Leveling of a 2D Liquid Longitudinal and Shear Wave Sound Speed in a 2D Lattice Mechanical Properties of a 2D Numerically Modeled Lattice Vibration Frequencies of a 2D Numerically Modeled Lattice Damped Harmonic Oscillator Motion and Modes of a Particle in a Mexican Hat Potential Forced Oscillator Roller Bearing Cam and Roller Follower Simple Hybrid Gear Train Ratchet Animation Child's Swing Height Increase Mechanics Roller Chain Animation Elasticity of 3D Gas Driving a Piston Free to Forced Harmonic Oscillator Transition Physics of Mounting a Tire on a Rim Physics of a Pendulum Clock Escapement Physics of a Gas Pressure Gauge
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Physics of a Gas Pressure Gauge Ion Drift in Neutral Particle Sea Diffusion Equation Solved by Finite Difference Method Linear Particle Diffusion Heat Flow 1D with Time Dependent Boundary Solid Cube in Liquid Column Drag on a Large Sphere Due to a Digital Gas Animation of a Gas Centrifuge Laminar Flow of a Gas in an Annular Space Laminar Flow of a Fluid in a 2D Bearing Incompressible Fluid Flow through a Constriction Fluid Flow Due To Pressure Gradients
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Parallel Resistors Gas Discharge Animation Oscilloscope Animation Permanent Magnet in Solenoid Cross Product of Two Vectors Magnetic Braking with Cylindrical Geometry Stopping a Falling Magnet by Eddy Currents Magnetic Brake Magnetic Field of a Long Solenoid Coil Light Propagation in a Transparent Dielectric Material Dipole Array Animations Angular Distribution of Emission of Arrays of Excited Dipoles Geometric Derivation of Snell's Refraction Angle Law Electromagnetic (EM) Wave Response to a Row of Dipoles Electromagnetic (EM) Wave Response to a Single Dipole Optics of a Transparent Plate by Iterating the Maxwell Wave Equation Diffraction by Iterating the Maxwell or Schrodinger Wave Equations Lens Focusing by Iterating the Maxwell or Schrodinger Wave Equations Optical Wave Packet Propagation by Finite Difference Matrix 1D Potential(x,y) Using Laplace's Equation Div(gradV)=0 with Variable Boundary Geometry Potential(x,y) Using Laplace's Equation Div(epsilon*gradV)=0 Laplace's Equation Div(gradV)=0 with Mixed BCs Potential(x,y) for Surface Electrodes with Dielectric Slab Dipolar Media Field Plots LCR Oscillator Animation Beam Trajectory of a Moving Laser Beam Trajectory in a Square Ring Laser Doppler Effect Converting Magnetic Forces to Electric Forces Converting Permanent Magnet Orbital Moments to Solenoid Currents Electron Beam Collimation by Axial Magnetic Field Electron Buncher for Klystron Charged Particle Spatial and Speed Bunching Electrical Conduction-Particle Picture Electromagnetic Bell Triode Vacuum Tube
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
E=mc^2 and Mexican Jumping Bean Radar Pulse Return Time Interval Experiment to Determine Gamma Current Loop with a Rotating Test Particle Moving Fabry-Perot Interferometer Space Time Invariant Intervals of a Moving Clock Relativity Transformations by Requiring Simulataneity Accelerated Space Trip Clock Times and Rates Minguzzi Invariant Inertial Frame Time Accelerated Space Trip with Light Pulse Signaling
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Solar Power Generation Planet Formation Illumination of Planets Change of Orbit due to Asteroid Impact Earth Time Zones Day Lengths Astronomical Aberration Kepler Planetary and Sun Orbits Model of Ocean Tides Gravity Course Iteration Spacecraft Speed Assistance by Gravity Hohmann Transfer from One Circcular Orbit to Another Star Distances Using the Parallax Method
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Semiconductor Electron Energies and Band Gap 1D Semiconductor Electron Energies and Band Gap 2D Simple Fermi Surface p-nJunctionDiode Depletion Width Temperature Dependence of 2D Fermi-Dirac Particles
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Assembly of 3D Parts Using Javascript Web Graphics Library 3D Compared to Javascript 3D Graphics 3D Graphics Tutorial Beginnings Proof of Pythagoras a^2+b^2=c^2
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Multiple Slider Animation Template for Plotting with HTML Enhanced Sliders or Ranges Collapsible Dropdown Menu Example Arrow Functions Fast Fourier Transform (FFT) Demonstration
Animation of a Progress Bar
Template for Scientific Plots
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Time Dependent Wave Equation 1D One Dimensional Optical Resonator Modes
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Probability of Birthday Match Random Creation of Probability Function Profiles Two Dies Probability Distribution Three Dies Probability Distribution
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Light Rays in a Transparent Isosceles Prism Light Ray in a Series of Wedges of Various Index of Refraction Snells Law of Refraction Refraction Due to Dipoles in Two Media Refraction and Reflection Two Media Animation of Concave Mirror Reflection Animation of Convex Lens Refraction Prism Refraction-Wave Picture Thick Lens Ray Trace Monochromator (Czerny-Turner Type) Wavelets from Concave Mirror> Thick Lens Focusing
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Sagnac Effect Fiber Optical Gyro (FOG) Ring Laser Gyro (RLG)
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Paticle Motion in a Venturi: Wall Reflections Paticle Motion in a Venturi Potential Elliptical Ion Trap Using Boundary Potential Distribution Prediction of Hard Disc Collision Time and Position Rigid Rotor Collisions
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Acoustic Wave with Built-in Pressure Acoustic Waves in 2D Numerically Modeled Solid Wave 1D on a Linear Array Waves on Discrete Model of Vibrating String Linear Acoustic Wave in a 3D Gas Spherical Acoustic Wave in a 3D Gas Laterally Perturbed Two Dimensional Gas with Lennard Jones Repelling Forces Longitudinally Perturbed Two Dimensional Gas with Lennard Jones Repelling Forces
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Bicep and Forearm Animation Blood Pressure Measurement Multiple Dose Residual Medicine Vs Time The Eye and its Resolution Breathing Animation Scoliosis Animation Muscle Animation
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Scattering from a Crystalline Target 2D Scattering from a Crystalline Target 3D
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12
Energy Conduction in a 2D Numerically Modeled Solid Lattice Unbalanced Gas Dynamics:Energy Flow in a Gas
Chapter 4
Chapter 5
Chapter 6
Chapter 7
Chapter 8
Chapter 9
Chapter 10
Chapter 11
Chapter 12

Hover over the menu bar to pick a physics animation.

Crystal Target Scattering Angular Distribution

This animation is similar to the Rutherford scattering experiment. The Rutherford scattering experiment (RSE) is famous because it established that atoms of a solid have a very compact nucleus. In the case of the RSE, the solid was a very thin gold foil and the incident particles were doubly ionized helium atoms (nucleii) which are also called alpha (`alpha`) particles. The molecule weight of gold is 197 and that of helium is 4. Therefore, if almost all the mass of the gold atom is concentrated in its small nucleus, when the alpha particle hits the gold nucleus, only a small fraction of its energy will be transferred to the nucleus. If the alpha particle hits the gold nucleus dead center, then the alpha particle will bounce back 180 degrees from its original direction. It turned out that that is what happened. It led to Rutherford making the now famous comment:

"It was quite the most incredible event that has ever happened to me in my life. It was almost as incredible as if you fired a 15-inch shell at a piece of tissue paper and it came back and hit you."

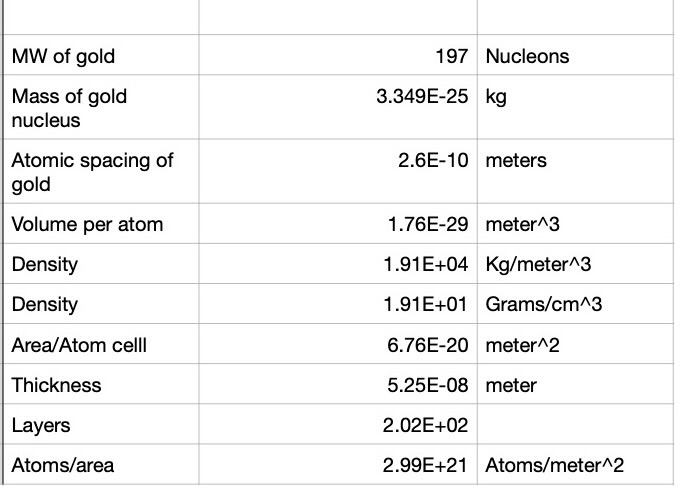
This result would not have been the case if the nucleus were not extremely compact. It turns out that the nucleus mean radius is of the order `r_(n)=10^(-14) ` meters. Gold has a face centered cubic (FCC) crystal structure where the cube edge is `a_(gold)=4.07cdot10^(-10)` meters. So viewed from the side, as seen in Canvas 0, the spacing between each gold atom occupies an area of 1/2 the area of a square of edge length `a_(gold)` so each gold atom occupies an area `A_(gold)=(16.56/2)cdot10^(-20) meters^2` (see Spreadsheet 0) . This means that it will be extremely unlikely that a small alpha particle would have a hard collision with a helium nucleus. In fact, the probability, P, is about

`P=(pi r_n^2)/A_(gold)=3.5 cdot 10^(-9)`

and yet a significant fraction of the alpha particles were deflected at other than small angles. Part of the reason for that is that the alpha particle did not have to actually contact the nucleus of gold since both have fairly large positive charge. The charge of gold is `Z_(gold)=79` while that of the alpha particles is `Z_(alpha)=2` where the Z values represent the number of oppositely signed electron charges, `e`, where `e=1.6cdot10^(-19)` coulombs.

With that introduction, we are now ready to work out the details of this animation. The illustration in Canvas 0 shows only a single layer of gold nucleii. An actual gold foil will have at least `n_L=200` layers so the probability of a direct hit is increased by `n_L` or to `P=0.7 cdot 10^(-6)` if `n_L=200`.

Spreadsheet 0: Gold Foil Target Spreadsheet
Canvas 1: Diagram Showing Impact Parameter
Impact Radius 50
Sphere Radius 50
Canvas 0: Diagram of Gold Crystal Geometry
Number of Unit Cell Columns or Rows
Canvas 2: Particle Scattering Animation
Beam-Target Opacity: 0.5
Single Step
Canvas 3: Plots of Scatter Vs Angle .

Equations for the Animation and Plots

Below I show that, when the target particle is much more massive than the beam particle as is the case for alpha particles incident on gold nucleii, the change in angle of the scattered particle is just twice the incident angle. The incident angle is defined as the angle between the incident velocity and the vector between centers of the beam and target particles when they have just achieved contact. See a diagram of these angles in Canvas 4. Then, using equations similar to bouncing off of a flat wall, the final beam particle velocity vector `bb v_f` becomes:

`bb v_f=bb v_i-2 hat bb"u" ( bb v_i cdot hat bb"u") `

where `bb v_i` is the incident velocity and `hat bb"u"` is a unit vector pointing from the target particle to the beam particle. Note that this equation conserves energy

`(bb v_f cdot bb v_f) =(bb v_i cdot bb v_i)`
` -4 (hat bb"u" cdot bb v_i) ( bb v_i cdot hat bb"u")`
`+4 (bb v_i cdot hat bb"u" ) (bb v_i cdot hat bb"u") =(bb v_i cdot bb v_i)`

` Also this equation is correct even when the beam particle makes multiple scatterings from the target particles even when the initial velocity is not along the x axis.
This equation gives the final velocity for each time a beam particle contacts a target particle. Then the beam particle position is iterated using this new velocity.

`x_p=x_p+v_xdt`
`y_p=y_p+v_ydt`

where `dt` is the iteration time increment. When the particle reaches the circular chamber wall, it is stopped. Then particle numbers that have reached the wall are placed in bins Vs their angle on the wall. A plot of bin occupation Vs angle is shown in Canvas 3. The same bin accumulation data is shown in Canvas 2 in a circular plot where the highest bin count is shown at the center of the scatter chamber. The learner has the option of adjusting the target opacity. This depends on both the target particle radius, `r_t`, and particle spacing `s_t` and the beam particle radius, `r_b` via the expression:

`s_t=2.5/(opacity)*(r_t+r_b)`;

where the 2.5 factor is just a parameter that seems to make the ratio of forward scatter to backscatter agree with the numerical results.

Discussion of the Animation Results

First I should say that this is a 2D animation while the Rutherford experiment was a 3D experiment. The 2D here means that the target nucleii are really cylinders along the z axis and perpenducilar to the x and y axes. Also the "gold" nucleii that we use here are much larger compared to their spacing than the nucleii in a real gold foil. This is necessary in order to show at least some backscattering in a finite time. We expect, with target opacity of 50%, to have about half of the beam particles go right through the target without being deflected. As you can see by looking at Canvas 3 after the Run has is complete, that is fairly reasonably valid.
Canvas 4: Diagram Showing Incident and Scattering Angles
Impact Radius 50

Deriving the Equations for Final Velocities After Collision

In the following equations, please be aware that bold letters denote vectors which have either (x,y) or (x,y,z) components depending on whether we are considering 2D or 3D calculations. For hard sphere collisions one must consider both conservation of momentum and energy. If the collision was mediated by a potential between the particles, one would only have to consider conservation of kinetic and potential energy. Conservation of momentum requires that the final momentum be the same as the initial momentum. For a collision between particles 1 and 2:

`m_1 bb"v"_{1f}+m_2 bb"v"_{2f}=m_1 bb"v"_{1i}+m_2 bb"v"_{2i} (1)`

where the subscript f stands for final value and the subscript i stands for initial value and the arrowed bold letter ` bb"v"` stands for the velocity vector. The conservation of kinetic energy equation is as follows:

`m_1 bb"v"_{1f} cdot bb"v"_{1f} +m_2 bb"v"_{2f} cdot bb"v"_{2f}`

`=m_1 bb"v"_{1i} cdot bb"v"_{1i} +m_2 bb"v"_{2i} cdot bb"v"_{2i} (2)`

where the `cdot` between the velocity vectors stands for the inner or dot product of the two vectors. When we combine equations 1 and 2 we get equations that relate the components of the velocity vectors.

The most important concept in these calculations is that of the unit vector ` hat bb"u"` between the centers of the two particles that are colliding

` hat bb"u"=[(x_2-x_1)hat bb"x"+(y_2-y_1)hat bb"y"+(z_2-z_1)hat bb"z"]/r_{12}`

where the x, y, and z that have hats are unit vectors along their respective axes and

`r_{12}=sqrt[(x_2-x_1)^2+(y_2-y_1)^2+(z_2-z_1)^2]`

Note that the unit vector points from sphere 1 to sphere 2 so, if `x_2` is greater than `x_1`, the unit vector's x component is positive.
Applying equation 1, we know that the changes of momentum of the spheres are equal and opposite and are along the unit vector `hat bb"u"` so we can write:

`m_1 delta bb"v"_1=M delta v hat bb"u"=-m_2 delta bb"v"_2 (3)`

where `M` has units of mass and `M` and the scalar speed increment `delta v` are still to be determined. Now we may re-write equation 2 using equation 3 and obtain:

`((m_1 bb"v"_1+M delta v hat bb"u") cdot (m_1 bb"v"_1+M delta v hat bb"u"))/(m_1)+ ((m_2 bb"v"_1-M delta vhat bb"u") cdot (m_2 bb"v"_2-M delta vhat bb"u"))/(m_2) =m_1 bb"v"_{1} cdot bb"v"_{1} +m_2 bb"v"_{2} cdot bb"v"_{2}(3)`

After cancellations of the terms on its right side, equation 4 simplifies to:

`M delta v=(2m_1m_2)/(m_1+m_2)( bb"v"_1- bb"v"_2) cdot hat bb"u"`

We can now make the identifications:

`M=(2m_1m_2)/(m_1+m_2)`

and

`delta v=( bb"v"_1- bb"v"_2) cdot hat bb"u"`

where M is known as the "reduced mass" Finally using equation 3 again we can write the expressions for the final velocity vectors:

` bb"v"_{1f}= bb"v"_{1i}+M/m_1 [( bb"v"_1- bb"v"_2) cdot hat bb"u"] hat bb"u" (5)`
` bb"v"_{2f}= bb"v"_{2i}-M/m_2 [( bb"v"_1- bb"v"_2) cdot hat bb"u"] hat bb"u"`

When `m_2/m_1 gtgt 1` then `M/m_1` becomes 2. We use equation 5 with `M/m_1=2` to compute the scatter direction of the beam particles.
As always, the learner is encouraged to press F12 (Windows) and select "Sources" to examine the HTML and javascript code that was used to create this page.